Inscription / Connexion Nouveau Sujet
Démontrer position relative entre tangente et courbe
bonsoir,
alors voila je suis en Term Es et j'ai un DM a rendre mais je bloque sur la dernière question de l'un de mes exercices 
voila l'exercice:
f est la fonction définie sur }0;+infini{ par f(x)= 2lnx - 1
question 1 : déterminer équation tangente au point abscisse 1
réponse : j'ai utilisé la formule f'(a)(x - a)+f(a) et j'ai trouvé T0: y= 2x - 3 (résultat vérifié en traçant la courbe sur ma calculatrice)
question 2 : conjecturer la position relative entre la courbe représentatrice de la fonction f et la tangente
réponse : la tangente semble au dessus de la courbe sur le graphique sur l'intervalle }0+infini{
question 3 : démontrer la conjecture de la question 2
c'est içi que je coince... Je ne vois pas comment confirmer ma conjecture... j'avais l'idée de faire f(x)<t(x) en disant que t(x) et la fonction représentée par la tangente mais je ne sais pas comment m'y prendre et surtout je ne sais pas si c'est se que je dois faire
merci de m'éclairer
Bonsoir,
détermine le signe de f(x)-(2x - 3 )
tu pourras conclure car :
si f(x) -(2x-3 )> 0 alors f(x)>2x-3 donc la courbe est .................... de la tangente
si f(x) -(2x-3 )< 0 alors f(x)<2x-3 donc la courbe est .................... de la tangente
merci  j'ai compris
j'ai compris
si f(x) -(2x-3 )> 0 alors f(x)>2x-3 donc la courbe est au dessus de la tangente
si f(x) -(2x-3 )< 0 alors f(x)<2x-3 donc la courbe est en dessous de la tangente
donc:
f(x)- 2x - 3
= (2lnx - 1)-(2x - 3)
= 2lnx - 1 - 2x + 3
= 2lnx - 2x + 2
= ?
et la je fais comment ? je ne peux pas me débarasser du lnx et du x donc je ne peux pas savoir si le résultat est positif ?
2lnx - 2x + 2 =2(ln(x)-x+1)
signe de ln(x)-x+1
g(x)= ln(x)-x+1
g'(x)=\dfrac{1}{x}-1=\dfrac{1-x}{x}
g'(x)≥0 si 1-x≥0 si x≤1
g' s'annule et change de signe pour x=1 donc g admet en maximum en 1
g est croissante sur ]0;1]
g(1)=0
g admet un maximum de 0 en 1
2ln(x)-2x-2≤0 la courbe est en dessous de la tangente
merci beaucoup 
alors j'ai essayé de reprendre l'exo enfin la question 3 pour bien comprendre mais il y a quelque chose que je ne comprend pas
j'arrive à retrouver f(x)-(2x-3) = 2(lnx-x+1) jusque là c'est bon
Ensuite je sais qu'il faut que je m'intéresse au signe de lnx-x+1 qu'on appellera g(x) puisqu'on sait déjà que 2 est positif.
Pour trouver le signe je cherche la dérivée g'(x)= 1-x / x je trouve le même résultat
C'est la que je ne comprend pas tout,
j'ai fais g(x)= 0 et j'ai trouvé x=1 donc g(x) s'annule et change bien de signe pour x=1 et g(1)=0
mais ensuite je trouve l'inverse, pour moi c'est un minimum et g(x) est décroissante sur {0;1}
enfin c'est ce que je vois dans mon tableau :
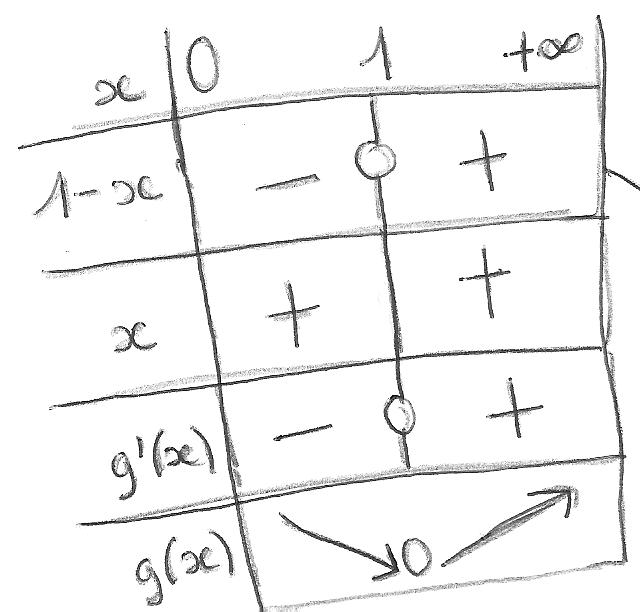
désolé pour la taille de l'image :S
autrement dit si x<1
1-x est positif si x est compris entre 0 et 1
s'annule pour x=1
et est négatif pour x supérieur à 1


