Inscription / Connexion Nouveau Sujet
Démontrer une inégalité avec une intégrale.
Bonjour, je débute dans les intégrales, j'espére que vous pourrez m'aiguiller sur un exemple d'inégalité que je donne ci-dessous.
Je cherche à démontrer cette inégalité :  -(ln2)/2
-(ln2)/2
Avec 0.5 en bas et 1 en haut, je maitrise pas trop les commandes Latex. :s
Merci.
Edit Coll : LaTeX
Salut
autre que la méthode géométrique tu peux commencer comme cela:
, tu applique ln qui est croissante puis tu intègre entre 0,5 et 1 ettt voilà ton encadrement

Je ne crois pas que l'indication de monrow soit suffisante.
Non, mais la représentation graphique te donne des indictions sur la manière de faire.
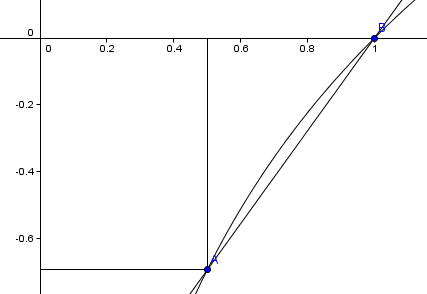
Quelle est l'équation de la droite (AB) ? appelons là y=ax+b
Comment montrer que sur l'intervalle on a
Peut-être as-tu vu une autre inégalité en cours qui peut t'aider.
et donc, la surface algébrique (l'intégrale) entre l'axe Ox et la courbe sera supérieure à celle entre l'axe et la droite.
Il te reste à calculer cette dernière.
C'est possible de diviser par deux que d'un coté. Je parle des deux derniéres étapes des inéquations.
A voui, trés juste... je vais essayer de m'en coller deux ou trois sur le même modéle. Sa devrait finir par rentrer. ^^
Merci pout votre aide.
A bientôt.
Autant pour moi, je voulais majorer la somme.
La question est de la minorer., Et ta solution est parfaite.
Désolé.