Inscription / Connexion Nouveau Sujet
Déplacement sur un cercle trigonométrique
bonjour a tous j'ai besoin de votre aide sa serai sympa^^
Le point M, image d'un réel x,se déplace sur un cercle trigonométrique.
1.Dans chacun des cas suivants,colorer sa trajectoire,indiquer le sens de déplacement et de quelle valeurs a quelle valeur varie x.
a) x
[-
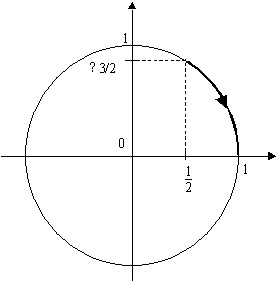
;],cos(x) croît de 1/2 à 1 et sin(x) décroît de 
3/2 à 0.
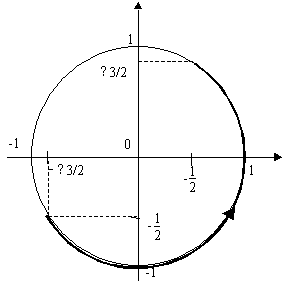
b)x[0;2], cos(x) décroit de 1/2 à -1,puis croît de -1 à 0 et sin(x) croît de 3/2 à 1, puis décroît de 1 à -1
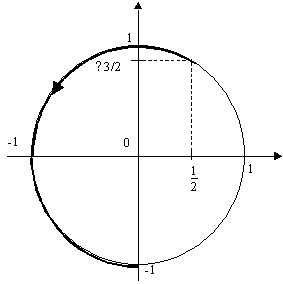
c) x[-;],cos(x) croît de -3/2 à 1/2 et sin(x) décroît de -1/2 à -1,puis croît de -1 à -3/2.
merci d'avance
bonjour
Pour le a)
tu places le point du cercle trigo de coord (1/2;3/2), puis le point de coord (1;0)
Sur l'axe des abscisses x varie de 1/2 à 1
sur l'axe des ordonnées y varie de 3/2 à 0
tu en déduis la trajectoire et le sens de déplacement
Pour les valeurs de x
quel x donne cos(x) = 1/2 et sin(x) = 3/2 ?
cos(x) = 1/2 donc x = pi/3 à 2pi près ou x = -pi/3 à 2pi près
sin(x) = 3/2 donc x = pi/3 à 2pi près ou x = pi - pi/3 à 2pi près
donc finalement x = pi/3
le truc c'est que j'ai du mal a placé les points =s
Les points sont sur le cercle trigo (cercle de rayon 1 cm de centre (0;0))
tu traces le cercle
tu places sur l'axe des abscisses une marque à 1/2
idem sur les coordonnées à 3/2 (environ 0,87)
tu obtients ton point sur le cercle
tu n'aurai pas un dessin ou quelque chose comme sa pour me montrer pare que j'ai du mal al je n(y arrive pas et je ne comprend pas =s
oh mici t'es un amour donc sa c'est pour la a) c'est sa et donc je dois placé les point d ela meme facon??
Je ne comprend pas
donc je dois placé les point d ela meme facon?
les point placé sur le cercle 3/2,1,1/2... je les places exacetment pareille ??
Oui
En fait tu fait exactement la même chose.
et pour le b) et le c) si c'est pas trop demander 
ui jve bien mais bon il faut dire que ne math je suis pas 
plutot linverse je ne suis pas doué =s
franchement je suis certain que tu peux placer pour le b) les points :
(1/2;3/2)
(-1;0) (je pense qu'il y a une erruer dans ton énoncé)
(-1;0)
et (0;1)
je pense qu'il y a une erreur dans ton énoncé
cos(x) décroit de 1/2 à -1,puis croît de -1 à 0 et sin(x) croît de 3/2 à 1, puis décroît de 1 à -1
je pense que c'est
cos(x) décroit de 1/2 à -1,puis croît de -1 à 0 et sin(x) croît de 3/2 à 0, puis décroît de 0 à -1
non c'est exactement ce qu'il ya ecrit peut etre ils se sont trompé
Non c'est moi qui déconne.
je t'envoie un dessin pour me faire pardonner
voila le b)
Les angles (le x) de départ est le même qu'un a)
l'arrivé est
cos(x)= 0 donc x = pi/2 ou 3pi/2 à 2pi près
sin(x)=-1 dons x = 3pi/2 à 2pi près
donc x = 3pi/2
mdr tu ma fais peur lol merci et pour le c lol
pas compris surtout =s et pas trouver aussi =s
et il vari de ou a ou c'est vraiment gentille de ta par en tout qu'a de m'aidé 'est vraiment gentille ^^
il varie de
cos(x) = -3/2 donc x = 2pi/3 à 2pi près ou x = -2pi/3 à 2pi près
sin(x) = 1/2 donc x = -pi/3 à 2pi près ou x = pi - (-pi/3) à 2pi près
donc x démarre à -2pi/3 (=4pi/3)
jusque déjà vu au a)
Annuler
connectez vous