Inscription / Connexion Nouveau Sujet
Dérivabilité d'une fonction valeur absolue
J'ai un souci au niveau de cet exercice, si vous pouvez m'aider, ca serait vraiment sympas...
Je pense que cette fonction valeur absolue n'est pas dérivable, mais je trouve le contraire...Merci d'avance, toutes vos réponses sont les bienvenues !
f est la fonction définie sur R par f(x) = valeur absolue de (x[sup][/sup]-1)
1. Tracer la courbe C. On note le point A de C d'abscisse 1.
( jusqu'à la, c'est bon...)
2. a. Montrer que f est dérivable à droite en 1.
( est ce qu'il faut calculer la limite de f(x) quand x tend vers 1 ou vers 0 ? )
lim [f(x)-f(1)]/(x-1)= lim 1/ (x-1) = 1
x->0 x->0
x>0 x>o
f est donc dérivable en 1 de nombre dérivé 1.
(en revanche, si on calcule la limite de f(x) quand x tend vers 0, on obtient + l'infinit : f n'est alors pas dérivable en 1)
b. Déterminer une équation de la tangente à droite à la courbe C au point A. Tracer cette tangente.
( comment dériver une fonction valeur absolue ?...)
3. a. Montrer que f est dérivable à gauche en 1.
raisonnement analogue à 2.a.
lim [f(x)-f(1)]/(x-1)= lim 1/ (x-1) = 1
x->0 x->0
x<0 x<o
f est donc dérivable en 1 de nombre dérivé 1.
b. déterminer une équation de la tangente à gauche à la courbe C au point A. Tracer cette tangente.
4. La fonction f est-elle dérivable ?
( je pense que la fonction f n'est pas dérivable, mais j'ai trouvé le contraire, puisque j'arrive à f dérivable à gauche et à droite en 1 de même nombre dérivé 1...)
Bonsoir
f(x) = valeur absolue de (x[sup][/sup]-1)
quelle est ta fonction ??
si ta fonction est bien f(x) = |x-1| alors f(x) = x-1 pour x
1 dont la dérivée y = 1 et f(x) = -(x-1)=-x+1 pour x>1 dont la dérivée y = -1 .
comme la dérivée à gauche de 1 est différente de la dérivée à droite de 1 elle n'est pas dérivable en 1
A+
ma fonction est f(x) = |x2-1|
Bonsoir
Ah bon soyons donc attentif à l'énoncé
pour f(x) =|x²-1|
f(x)= x²-1 pour x 
-1 ou x 1 dont la dérivée est y' = 2x et pour x=1 ça fait 2 qui est la dérivée à droite de 1
2)b)l'équation de la tangente en 1 à droite est y = 2x-2
f(x) = -x² + 1 pour -1 < x < 1 et dont la dérivée est y' = -2x et pour x = 1 ça fait -2 qui est la dérivée à gauche de 1
=> f(x) n'est pas dérivable en 1 car le dérivée à gauche de 1 est différente de la dérivée à droite de 1
f(x) est dérivable partout sauf en -1 et 1
A+
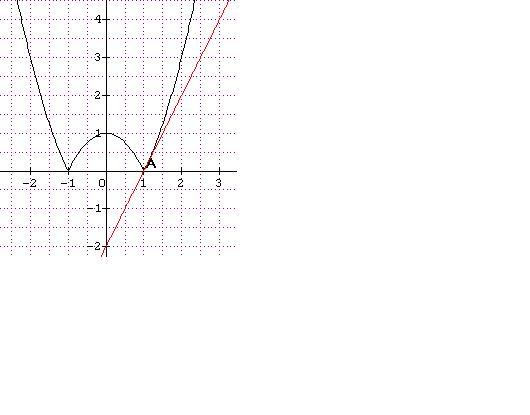
rebonsoir
la droite tracée en rouge dans mon post précédent est la tangente à droite de 1
Quant à l'équation de la tangente à gauche de 1 c'est y = -2x+2
A+
Merci beaucoup pour ces explications...
ce n'était pas si compliqué que ca en fait ! 
je me demande quand même s'il ne faut pas justifier les réponses en utilisant le taux de variation
a+
Annuler
connectez vous