Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Limites de fonctionsTopics traitant de Limites de fonctions [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Dérivée d'une fonction et tableau de variation

Posté par
unbreak 12-09-12 à 12:42

Bonjour à tous,

J'ai besoin d'aide pour dérivée une fonction, puis pour dresser le tableau de variation.

Citation :
Pour tout entier naturel n\ge1 considère la fonction fn définie sur [0 ; 1].
La fonction est fn(x) = x^n \sqrt{1-x}.
Cn est sa courbe représentative.

Etude des fonctions fn, pour n\ge2 :
a) Montrer que, pour tout réel x de [0 ; 1[ : fn'(x) = \frac{x^{n-1} [2n - (2n+1)x]}{2\sqrt{1-x}}
b) Dresser le tableau de variation de fn.


C'est donc une étude de fonction tout simple, mais je bloque pour la dérivée, car que je tombe pas sur la même expression que dans la question a).

Je vous explique ce que j'ai fais :

Pour dériver fn, j'ai utilisé cette propriété : u x v = u'v + uv'
Je démarre donc sur (nx^{n-1})(\sqrt{1-x}) + (x^n)(\frac{-1}{2\sqrt{1-x}})

je mets tout au même dénominateur : \frac{(n.x^{n-1})(\sqrt{1-x})(2\sqrt{1-x})-x^n}{2\sqrt{1-x}}

j'enlève les racines du haut : \frac{(n.x^{n-1})(-2(x-1))-x^n}{2\sqrt{1-x}}

je continue pour que cela ressemble à l'énoncé : \frac{(x^{n-1})(n)(-2(x-1))-x^n}{2\sqrt{1-x}}

je développe : \frac{(x^{n-1})(-2xn + 2n)-x^n}{2\sqrt{1-x}}

et je tombe, au final, sur \frac{x^{n-1} [2n + (-2n)x] - x^n}{2\sqrt{1-x}}

Je ne trouve pas donc pas la dérivée de la question a).

Pouvez vous me donner une piste pour que je tombe sur ce même résultat ?

Merci par avance.

Posté par
mathafou Moderateurre : Dérivée d'une fonction et tableau de variation 12-09-12 à 12:50

Bonjour,

xn = x.xn-1 ...

Posté par
unbreakre : Dérivée d'une fonction et tableau de variation 12-09-12 à 17:59

Ah bon ?

Ouais enfin ça arrange pas ton mon résultat car je suis encore loin de la dérivée attendu

Posté par
mathafou Moderateurre : Dérivée d'une fonction et tableau de variation 12-09-12 à 18:06

tu cherches midi à quatorze heures
\frac{x^{n-1} [2n + (-2n)x] - x^n}{2\sqrt{1-x}} = \frac{x^{n-1} [2n + (-2n)x] - x.x^{n-1}}{2\sqrt{1-x}} et tu factorises xn-1

Posté par
unbreakre : Dérivée d'une fonction et tableau de variation 12-09-12 à 18:14

Oui j'avais bien compris mais comment je fais le lien pour trouver ce que l'on me demande ? Cad \frac{x^{n-1} [2n - (2n+1)x]}{2\sqrt{1-x}}

D'une part si je développe ce qu'il y a dans mon crochet je trouve 2n - 2nx. Alors que dans l'énoncé on a 2n -(2n+1)x ce qui donne 2n -2nx -x.

Et j'ai toujours le x.x^n-1 qui m'embête au bout.

Il doit y avoir une erreur non ?

Posté par
mathafou Moderateurre : Dérivée d'une fonction et tableau de variation 12-09-12 à 18:30

Il faut te faire tes factorisations ???

\frac{x^{n-1} [2n + (-2n)x] - x^n}{2\sqrt{1-x}} = \frac{x^{n-1} [2n + (-2n)x] - x.x^{n-1}}{2\sqrt{1-x}} = x^{n-1} [ ... ]
il n'y a pas de "x.xn-1" qui "traine au bout"

Posté par
unbreakre : Dérivée d'une fonction et tableau de variation 12-09-12 à 19:03

Oki merci je suis tombé sur la bonne expression

Pour le tableau, je trouve 2 valeurs à mettre, 0 et 1, mais ce sont justement les valeurs de l'intervalle, qui est [0 ; 1]. En plus dans cette dérivée il y a n comme autre inconnu.

Je n'arrive pas à réaliser mon tableau de variation

Comment je peux déterminer le signe de f'(x) sachant que je ne connais pas n ?

Posté par
mathafou Moderateurre : Dérivée d'une fonction et tableau de variation 12-09-12 à 19:12

dans [0, 1[ le signe de x est ... donc celui de xn-1 est ...
le signe du radical est ...

donc f' est du signe de 2n - (2n+1)x

faire intervenir la valeur 2n/(2n+1) donc dans ce tableau de variations.
0 < 2n/(2n+1) < 1 quel que soit n entier, donc cette valeur est bien dans l'intervalle étudié pour x [0, 1[
que cette valeur ne soit pas numérique importe peu non ? tu la fait figurer telle quelle dans le tableau.

Posté par
unbreakre : Dérivée d'une fonction et tableau de variation 12-09-12 à 19:44

D'accord merci pour ta réponse

J'ai donc une première ligne avec 0, 2n/2n+1 et 1 comme valeurs de x.
Une seconde ligne qui est le signe de f', qui lui même correspond au signe de 2n - (2n+1)x. Le signe est +.
Et enfin j'ai les variations de f, qui là est strictement positive, de 0 à 1 e, tout cas.

J'espère que c'est bien ça.

Je dois maintenant étudier la position relative de Cn+1 par rapport à Cn. Je pense faire fn+1(x) - fn(x) et étudier tout ça

Posté par
mathafou Moderateurre : Dérivée d'une fonction et tableau de variation 12-09-12 à 20:02

Citation :
qui lui même correspond au signe de 2n - (2n+1)x. Le signe est +


ah bon ???
Dans chacun des deux intervcalles [0, 2n/(2n+1] et [2n/(2n+1), 1[ ????
2n - (2n+1)x est toujours > 0 ???

Citation :
j'ai les variations de f, qui là est strictement positive,


"les variations de f" c'est "f est croissante, décroissante, constante"
que f soit positive ou pas est une autre question.

Pour la suite, oui, je pense qu'étudier fn+1(x) - fn(x) est une piste à suivre...

Posté par
unbreakre : Dérivée d'une fonction et tableau de variation 12-09-12 à 20:16

C'est pourtant bien ce qu'on a mis tout à l'heure :

Citation :
donc f' est du signe de 2n - (2n+1)x
non ?

Oui je voulais dire f est croissante, désolé

Je vais voir d'ici demain pour la représentation des courbes.

Posté par
mathafou Moderateurre : Dérivée d'une fonction et tableau de variation 12-09-12 à 20:27


mais le signe de 2n - (2n+1)x dépend de la valeur de x par rapport à 2n/(2n+1) !!!

si x < 2n/(2n+1) alors 2n - (2n+1)x est ???
si x > 2n/(2n+1) alors 2n - (2n+1)x est ???

Posté par
unbreakre : Dérivée d'une fonction et tableau de variation 14-09-12 à 16:23

bah si x < 2n/(2n+1)  alors 2n - (2n+1)x est positif
et si x > 2n/(2n+1)  alors 2n - (2n+1)x est négative

Du coup en dessous de 2n/2n+ je mets un zéro.

Quoiqu'il en soit la fonction est croissante sur [0;1] non ?

Pour la position relative des courbes Cn+1 et Cn, j'ai donc calculé fn+1 - fn et avec le résultat j'ai fais un tableau de signe.
J'ai vu que fn+1 < fn sur [0;1] donc que Cn+1 est en dessous de Cn sur [0 ;1].

Posté par
mathafou Moderateurre : Dérivée d'une fonction et tableau de variation 14-09-12 à 16:49

f'(x) est donc (c'est toi-même qui l'a dit) >0 si x < 2n/(2n+1)
donc f(x) est ???
mais
f'(x) est (idem) <0 si x > 2n/(2n+1)
donc f(x) est ???

en d'autre termes tu as le tableau de variations de f(x) :

0 2n/(2n+1) 1
f'(x) >0 0 <0
f(x) croissante décroissante

(2n/(2n+1) est toujours entre 0 et 1 donc intervient dans le domaine considéré)

Les courbes représentatives de f pour n = 0, 1, 2, 3
et leurs maximas en 2n/(2n+1) (sauf pour n = 0 )
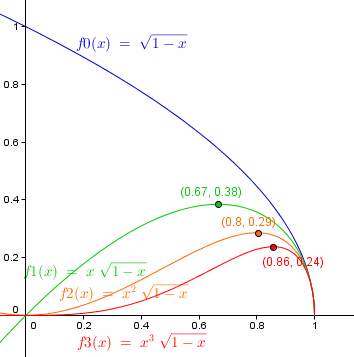
Dérivée d\'une fonction et tableau de variation

On "voit" que c'est bien comme demandé (que Cn+1 est toujours "au dessous" de Cn)
et si tu as fait les calculs le prouvant, c'est OK.

Posté par
unbreakre : Dérivée d'une fonction et tableau de variation 14-09-12 à 17:26

D'accord je comprends mieux.

Oui pour la position relative des courbes j'ai bien tout pour prouver.

Merci beaucoup à toi !


Rechercher
Menu
Espace membre
29 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1724 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !