Inscription / Connexion Nouveau Sujet
dérivée seconde ; position courbe/tangente
Bonjour,
Je rencontre des difficultés pour la résolution d'un exercice de maths dans le chapitre fonction, variations et continuité. Nous avons (avec un camarade) déjà répondu à un certain nombre de questions, mais là nous bloquons ...
Voici l'énoncé et ce qui a déjà été fait :
g une fonction dérivable deux fois sur I. D sa courbe représentative dans le repère orthonormal (O,
,
)
Soit b un réel de I et T la tangente à D au point B(b;f(b))
Pour tout réel x de I, on note N le point de D d'abscisse x et L le point de T d'abscisse x
1. (fait) : On a justifié que = d(x)
, où :
d(x) = g(x)-g'(b)(x-b)-g(b)
2. Dans cette question, on suppose que g'', dérivée seconde de g, est tel que g'' 
0 sur I
a. (fait) On a étudié les variations de d sur I ce qui donne :
décroissant pour x<b
0 pour x=b
croissant pour x>b
b. (fait) On en a déduit que D est au dessus de toutes ses tangentes
3. (fait) On a étudié de manière analogue la position de D par rapport à ses tangentes dans le cas où g" 
0 sur I
Cela a donné :
croissant pour x<b
0 pour x=b
décroissant pour x>b
C'est à partir de là que nous bloquons :
4. On suppose dans cette question que :
si x 
I et x b alors g"(x) 0
si x I et x b alors g"(x) 0
Démontrer que le point A est un point d'inflexion de la courbe D.
Je sais l'exercice est presque fini, mais nous n'arrivons pas à trouver ... J'espère que vous pourrez nous aider. Merci d'avance.
Bonjour
En effet, c'est fini! Si vous (vous êtes nombreux?) avez bien compris que le signe de d(x) donne la position de la courbe par rapport à la tangente, que d'(x)=g'(x)-g'(b) et que d''(x)=g''(x), ça marche pareil. Avec les hypothèses de 4, d' est d'abord décroissant et ensuite croissant. Comme d'(b)=0, ça montre que d' est positif. Donc d est croissant. Comme d(b)=0, d est d'abord négatif et ensuite positif, donc la courbe est d'abord au-dessous de la tangente et ensuite au-dessus. Elle traverse sa tangente! (c'est ça un point d'inflexion).
Voici un exemple: b=1
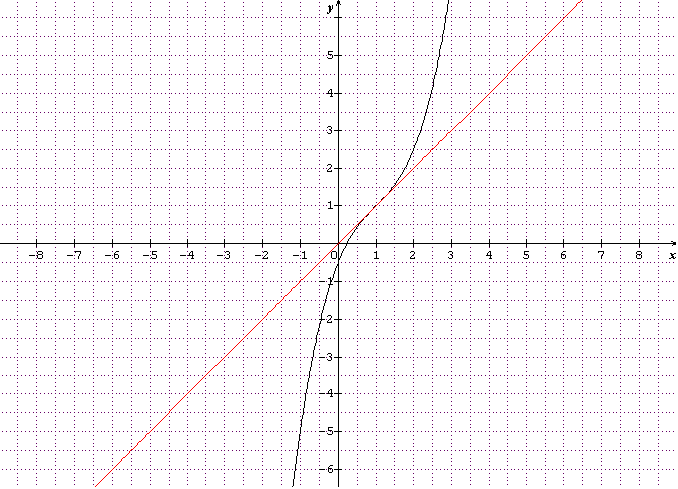
merci de votre réponse. En fait, si on veut déterminer la position de la courbe par rapport à ses tangentes pour une fonction donné défini sur un intervalle, il faut reproduire toutes les étapes précédentes ou seulement la dernière, celle que vous venez d'expliquer ? Par exemple pour :
f(x)=-x4 +4x+1 sur 
En fait l'étude générale a montré que cette position dépend uniquement du tableau des signes de la dérivée seconde.
D'accord ! Est ce que cela suffit de dire que :
pour une fonction f sur tel que f(x)= -x4+4x+1
f'(x)=-4x3+4
f"(x)=-12x2
Et qu'on ai le tableau de signe :
x<0 --> positif
x>0 --> négatif
Donc que la courbe est au dessus de ses tangentes sur ]-
;0[ et en dessous sur ]0;+[
ah ! c'est plus compliqué que je ne le pensais, il faut donc tout développer et factorisé mais merci beaucoup de votre aide !
Mais, la dérivée seconde est bien la dérivé de la dérivé non ? donc si on dérive
-x4+4x+1
ça donne en dérivé première :
-4x3+4
et en dérivant encore une fois on obtient :
-12x2
qui est la dérivé seconde non ? S'il vous plait expliquez moi si je me trompe !
OK! Elle est toujours au-dessus!Ce n'est pas grave, ça me rassure seulement que je comprenne ! Merci en tout cas de votre aide précieuse !
Annuler
connectez vous