Inscription / Connexion Nouveau Sujet
dérivées fonction
besoin d'aide stp !! il me manque les questions:
c) Justifier que la fonction f est une fonction "satisfaction"
2)
c) on admet que..
d) étudier la convexité
et
3) a partir de quelle durée 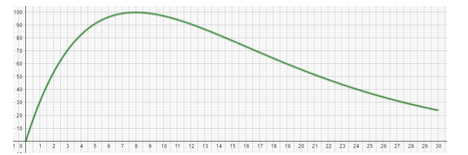
* Modération > Image recadrée, sur la figure uniquement ! Si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé en répondant dans le même sujet  *
*
bonjour
la fonction me satisfait bien ^^
sérieusement... quelle réponse attends tu avec un tel bout d'énoncé ?
lis ceci : ![]() Sujet ancien- ne plus donner ce lien-merci
Sujet ancien- ne plus donner ce lien-merci
points 0, 3 et 4
Bonsoir, il me manque quelques questions, besoin d'aide et de vérifications svp.. je met ce que j'ai trouvé déjà
On appelle fonction « satisfaction » toute fonction dérivable à valeurs dans l'intervalle 0;100 . Lorsque la fonction
« satisfaction » atteint la valeur 100, on dit qu'il y a « saturation ».
On définit aussi la fonction « envie » comme la fonction dérivée de la fonction « satisfaction ». On dira qu'il y a « souhait » lorsque la fonction « envie » est positive ou nulle et qu'il y a « rejet » lorsque la fonction « envie » est strictement négative.
1)On considère la fonction f définie et dérivable sur l'intervalle 0;3 par : f (x)12,5xe0,125x+1 .
a)Déterminer une expression de f ' (x) , la fonction dérivée de f, pour tout réel x de 0;30.
b)Etudier le signe de f ' (x)sur 0;30, puis dresser le tableau de variation de f sur 0;30.
c)Justifier que la fonction f est une fonction « satisfaction ».
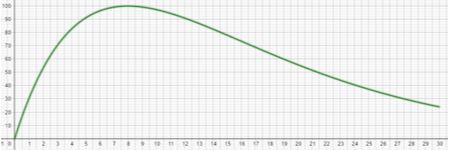
2)La directrice d'un réseau national d'agences de trekking utilise la fonction f définie ci-dessus et représentée ci- dessous pour modéliser la satisfaction de ses clients en fonction de la durée x de leur séjour, compris entre 0 et 30 jours.
a)A quel durée de séjour correspond l'effet « saturation » ? Justifier. b)A partir de quelle durée de séjour y a-t-il « rejet » ? Justifier.
c)On admet que la fonction f est deux fois dérivable surl'intervalle 0;30.
Montrer que, pour tout réel x de 0;30,
f ''(x)= -1,5625(2-0,125x)e0,125x+1 .
d)Etudier la convexité de f sur 0;30.
Préciser le ( ou les ) point(s) d'inflexion .
3)A partir de quelle durée de séjour peut-on estimer que la fonction « envie » se met à croître ? Justifier.
(je n'ai pas les crochets sur mon ordinateur 0;30 est l'intervalle... désolée !)
1) a) (eu)'= u'eu
(e-0,125+1)= -0,125e-0,125x+1
f'(x)= 12,,5e-0125+1+12,5x(-0,125=(12,5*O,125x)e-O,125x+1
f'(x)=(12,5-1,5625x)e-0,125+1
b) Pour tout réel de l'intervalle 0;30, e-0,125x+1>0 donc le signe de f'(x) est le signe de (12,5-1,5625x).
J'ai également fais les tableaux, celui des signes est celui de variation. il me manque la question c) svp pour l'instant
*** message déplacé ***
on est d'accord que pour cette question, je n'ai pas le droit d'utiliser le graphique ?
*** message déplacé ***
Vous dites bien que est définie sur
par
une fois on a une fois on a
laquelle est-ce ?
*** message déplacé ***
En considérant que c'est bien
est du signe de *******
*** message déplacé ***
malou edit > merci de ne pas faire l'exercice à la place du demandeur.
Si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé en répondant dans le même sujet
Je ne fais pas le sujet j'ai juste réécrit ce qu'elle avait effectué en simplifiant car il ne servait à rien de faire certaines multiplications
pour b il n'y avait pas besoin décrire tout cela j'ai juste mis ce qui était intéressant
Pour tout réel de l'intervalle 0;30, e^(-0,125x+1)>0 donc le signe de f'(x) est le signe de (12,5-1,5625x).
f'(x) est du signe de (12,5-1,5625x)e-0,125x+1
OUPS, désolée j'ai bien pris conscience de tout merci.
Il ne fallait pas effectuer certaines multiplications Ainsi on pouvait dire que c'était du signe de
question c) En quel point admet-elle un maximum et que vaut-il ?
Ensuite 2) dérivée seconde
Oui c'est bien ce qui est dit
On appelle fonction « satisfaction » toute fonction dérivable à valeurs dans l'intervalle [0;100]
je suppose que les crochets sont fermés
ensuite pour la
2) a)
Je vois sur le graphique que la fonction satisfaction f est croissante sur 0;8 et décroissante sur [8;30], or x=8 et f(8)=100
L'effet saturation correspond au jour 8 du séjour.
b) Grâce aux variations de la fonction "envie" on peut en déduire le signe de la fonction dérivée f'.
f' est positive sur[ 0;8 [ et négative sur ]8;30].
Il y a donc rejet au bout de 8 jours de séjour.
Jamais on voit que Commentaire : où est la boule de cristal ?
On a montré que admet un maximum en 8 qui vaut 100, or il y a saturation lorsque
donc il y a saturation pour
la durée est donc de huit jours
On a montré que la dérivée était strictement négative sur ]8~;~30] Par conséquent il y a rejet à partir du neuvième jour
non non, si ça ne vous dérange pas je continue je suis en train de réfléchir pour la c) pour vous proposer qlq chose..
parce que 12,5 est en facteur
j'avais commencé par le mettre de côté en dehors des grandes parenthèses ensuite j'ai mis en facteur et il ne restait alors que
il ne restait bien, que
pour déterminer le signe
Les dérivées ne changent pas au gré du temps
la dérivée d'un produit n'est la somme des dérivées
Vous avez dérivé correctement pourquoi est-ce différent pour
n'est que la dérivée d'une fonction
Ce qu'il fallait démontrer s'il n'y avait pas l'oubli d'un signe - dans l'exponentielle
dans votre dernier message vous avez oublié un signe
Certes cela a peu d'importance puisque l'on veut savoir quand


 ) :
) :


