Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Géometrie plane et dans l'espaceTopics traitant de Géometrie plane et dans l'espace [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Déterminer l'équation d'un ensemble de points

Posté par
Maesan 01-01-21 à 15:34

Bonjour en fait j'ai un problème dans cet exercice,merci de bien vouloir m'aider

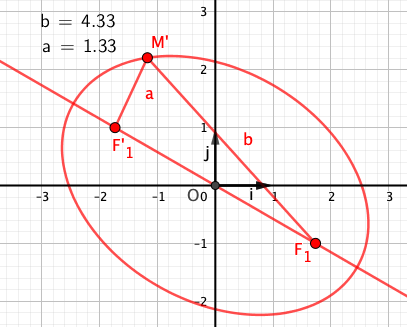
(O,i,j) est un repère orthonormé du plan.On considère dans ce repère les points F(√3,-1) et F'(-√3,1) .

u=((√3)/2)i-(1/2)j et v=(-1/2)u+(√3/2)j

(Je tiens à préciser que i,j,u et v sont des vecteurs)

a)Déterminer dans le repère (O,u,v) l'équation de l'ensemble E des points M(X,Y)  tels que MF+MF'=4√2

Bon j'ai commencer par écrire les coordonnées de F et F' dans (O,u,v) j'ai obtenu vect(OF)=(1/2)u et vect(OF')=(1/2)v

Arrivée à ce niveau j'ai voulu calculer la norme de vect(MF) vu que j'ai les coordonnées de F dans (O,u,v) ainsi que celle de vect(MF') mais quand je fais la somme et que je ppse égal a 5√2 je me retrouve avec des racines sur des X et d'autres non ,ça ne correspond pas à un ensemble précis.

Je ne sais pas si j'ai utilisé la bonne ressource pour la résolution de cet exercice.

Merci de m'aider.

Posté par
Maesanre : Déterminer l'équation d'un ensemble de points 01-01-21 à 18:07

Personne ne répond ,y'aurait il une erreur dans l'exercice?

Posté par
diracre : Déterminer l'équation d'un ensemble de points 01-01-21 à 18:15

Hello

Peut être pourrais tu partager tes résultats intermédiaires?

Posté par
diracre : Déterminer l'équation d'un ensemble de points 01-01-21 à 18:24

Sachant que \vec{OF'} =\frac{1}{2}\vec{v} est ... hasardeux

Posté par
Maesanre : Déterminer l'équation d'un ensemble de points 01-01-21 à 18:51

Bonsoir en fait je me suis rendue compte de mon erreur,vect(OF)=2u et vect(OF')=-2u, de là, je ne sais comment continuer

Posté par
diracre : Déterminer l'équation d'un ensemble de points 01-01-21 à 19:13

Aïe

Que valent MF et MF' dans le repère (O, , )?

Posté par
Maesanre : Déterminer l'équation d'un ensemble de points 02-01-21 à 05:00

Vect(MF)=(2-X)u-Yv et vect(MF')=(-2-X)u-Yv

D'ici j'ai essayé de calculer les normes et poser la somme égale à 4√2 mais je me retrouve avec des racines où il ne faut pas.

Comment je pourrais continuer s'il vous plaît?

Posté par
diracre : Déterminer l'équation d'un ensemble de points 02-01-21 à 08:14

Il est facile de se perdre dans ce calcul en effet ... (on verra ensuite une autre méthode "vectorielle" qui me semble plus "sympa")

A partir des expressions des 2 vecteur \vec{MF} et  \vec{MF'}

La propriété MF + MF' = 2\sqrt{2}

Doit te conduire à l'expression:

\sqrt{(x-2)^2+y^2}.\sqrt{(x+2)^2+y^2} = 12-x^2-y^2

Si non, tu as fait une erreur dans une étape intermédiaire du calcul

Si oui, tu continues sur ta lancée ... et tu élèves encore une fois au carré

Posté par
Maesanre : Déterminer l'équation d'un ensemble de points 02-01-21 à 08:19

C'était 4√2 d'accord je vais essayer comme ça

Posté par
diracre : Déterminer l'équation d'un ensemble de points 02-01-21 à 09:05

Pardon, 4\sqrt{2}, petite coquille: le 12 dans l'expression suivante est cependant bien obtenu avec cette valeur (sauf nouvelle coquille matinale ...)

Posté par
PLSVUre : Déterminer l'équation d'un ensemble de points 02-01-21 à 19:43

Bonsoir à vous deux,
@ Maesan
erreur de frappe :
\vec{v}=\red{\dfrac{-1}{2}\vec{u}}+\dfrac{\sqrt{3}}{2}\vec{j}

\vec{v}=\dfrac{1}{2}\vec{i}+\dfrac{\sqrt{3}}{2}\vec{j} \\
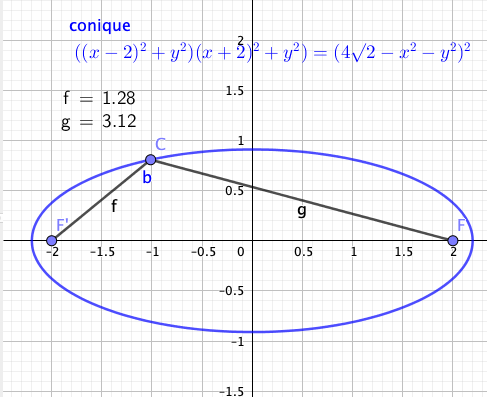
on peut obtenir  l'expression de la conique dans le repère (0,,) puis dans le repère (0,,)
@ dirac
ton expression ne convient pas .

Déterminer l\'équation d\'un ensemble de points

Déterminer l\'équation d\'un ensemble de points

Posté par
diracre : Déterminer l'équation d'un ensemble de points 02-01-21 à 20:29

Hello PLSVU

Si, si je te promets mon expression convient ...

Posté par
PLSVUre : Déterminer l'équation d'un ensemble de points 02-01-21 à 21:38

dans le repère (O,,)

Déterminer l\'équation d\'un ensemble de points

Posté par
diracre : Déterminer l'équation d'un ensemble de points 02-01-21 à 22:25

Hello

PLSVU ayant maintenant distillé le poison du doute , je vais prendre le soin de préciser que M a pour coordonnées (X,Y) dans le repère (0,,)


MF = \sqrt{(X-2)^2+Y^2}

MF' = \sqrt{(X+2)^2+Y^2}

Si MF + MF' = 4\sqrt2

En élevant au carré

MF^2 + MF'^2 + 2MFMF' = 32

Soit

X^2 -4X + 4 +Y^2 +Y^2+4X+4+Y^2 +2\sqrt{(X-2)^2+Y^2}\sqrt{(X+2)^2+Y^2} = 32

Et donc:

\sqrt{(X-2)^2+Y^2}\sqrt{(X+2)^2+Y^2} = 12 -X^2-Y^2

En élevant une nouvelle fois au carré:

X^4+4X^3+4X^2 +X^2Y^2-4X^3-16X^2-16X-4XY^2+4X^2+16X+16+4Y^2+X^2Y^2+4XY^2+4Y^2+Y^4 = 144-12X^2-12Y^2-12X^2+X^4+X^2Y^2-12Y^2+X^2Y^2+Y^4

Ce qui conduit à:

X^4-8X^2+2X^2Y^2+16+8Y^2+Y^4 = 144 -12X^2-12Y^2-12X^2+X^4+X^2Y^2-12Y^2+X^2Y^2+Y^4

En simplifiant une première fois:

-8X^2+8Y^2+16 = 144 -24X^2 -24Y^2

Soit

16X^2 +32Y^2=128

Soit

\frac{X^2}{8}+\frac{Y^2}{4} = 1

On reconnait là l'équation cartésienne d'une ellipse.

Je laisse à PLSVU le soin de commenter plus avant

Et à toi Maesan, le soin de vérifier tes/mes calculs

Ensuite je te proposerais une une autre méthode de détermination passant par un calcul vectoriel

Posté par
PLSVUre : Déterminer l'équation d'un ensemble de points 02-01-21 à 23:56

Salut dirac
  je n'ai pas fait aucun calcul, j'ai juste juste utilisé géogebra avec ton expression\sqrt{(x-2)^2+y^2}.\sqrt{(x+2)^2+y^2} = 4\sqrt{2}-x^2-y^2 ,avec la correction  que tu indiquais ,de remplacer le 12 par 4√2        ( j'aurais pas dû le faire...)
C'est pour cela que je me suis permis  d'intervenir
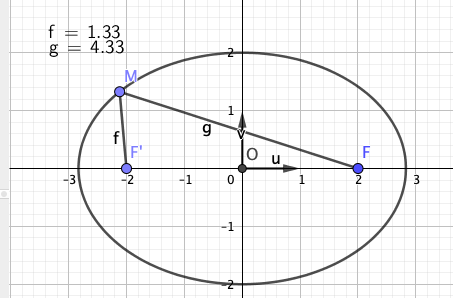
nous avons la même ellipse  dans le repère (O,u,v)  ,je l 'ai obtenue avec    deux calculs  ceux qui permettent    de trouver  le" 8 "et le "4" .
  et pour finir    celui pour avoir l'équation de l'ellispe dans le repère (0,i,j) (calculs de x et y)
Bonne fin de soirée.

Posté par
Maesanre : Déterminer l'équation d'un ensemble de points 03-01-21 à 12:45

Les calculs sont les bons je les ai vérifiés ,j'aimerais savoir comment utiliser le calcul vectoriel dans ce cas

Posté par
Maesanre : Déterminer l'équation d'un ensemble de points 03-01-21 à 12:51

Ensuite j'ai aussi un problème lorsqu'il s'agit d'écrire l'équation de de E dans (O,i,j)

Posté par
PLSVUre : Déterminer l'équation d'un ensemble de points 03-01-21 à 18:05

Je ne vois que la question 1a)
On considère dans ce repère les points F(√3,-1) et F'(-√3,1) .
u=((√3)/2)i-(1/2)j et v=(-1/2)u+(√3/2)j ????
a)Déterminer dans le repère (O,u,v) l'équation de l'ensemble E des points M(X,Y)  tels que MF+MF'=4√2
   Avant d'effectuer des calculs  concernant des mesures  de longueurs  dans le repère  (O,u,v),  tu dois vérifier .......
  L' énoncé dans son intégralité  est   utile   ainsi que les traces de tes recherches...
  

Posté par
diracre : Déterminer l'équation d'un ensemble de points 03-01-21 à 18:06

Ouf!

Citation :
Les calculs sont les bons je les ai vérifiés ,j'aimerais savoir comment utiliser le calcul vectoriel dans ce cas


Alors une autre méthode, un peu moins calculatoire que celle utilisée (qui, comme tu l'as vu, embarque des développements où l'on a vite fait de se perdre) est la suivante:

Tu remarques que \vec{MF} =   \vec{MF'} +  \vec{F'F}

Donc MF^2 - MF'^2 = 2 \vec{MF'} .\vec{F'F} + FF'2

Donc MF^2 - MF'^2 =  2\vec{MO} .\vec{F'F} +  2\vec{OF'} .\vec{F'F} + FF'2

Or O est le milieu de  [FF']  donc 2\vec{OF'} .\vec{F'F} = -FF'2

Donc en final  MF^2 - MF'^2 =  2\vec{OM} .\vec{FF'} = -8X

On a donc

MF + MF' = 4\sqrt{2}
(MF+MF')(MF-MF') = -8X

Soit

MF^2 = (2\sqrt{2} - \frac{X}{\sqrt2})^2 = (X-2)^2 + Y^2
MF'^2 = (2\sqrt{2} + \frac{X}{\sqrt2})^2 = (X+ 2)^2 + Y^2

Ces 2 équations menant à

8 +\frac{X^2}{2} = X^2 + 4 + Y^2

Et donc la même équation "réduite" que celle obtenue plus haut \frac{X^2}{8}+\frac{Y^2}{4} = 1

Là encore, on a vite fait de se perdre ... lorsque l'on ne sait pas où aller

C'est pour cela que PLSVU a un pris "tout droit" en reconnaissant dans  MF + MF' = 4\sqrt{2} la définition bifocale d'une ellipse  dont:
- on sait (lorsque l'on connait son cours ) que l'équation cartésienne réduite est  \frac{X^2}{a^2}+\frac{Y^2}{b^2} = 1
- a et b (les demi grand et petit axes) se déterminent en 2 calculs comme évoqué par les calculs des points d'intersections avec les axes OX et OY

Un exemple typique de situation où il vaut mieux maitriser le cours pour ne pas avoir à se cogner des lignes calculs   (bon, ceci étant, ici, il me semble que l'étude des coniques n'est plus au programme de Terminale depuis pas mal d'années )

Pour le passage en coordonnées cartésiennes de le repère (O, \vec{i}, \vec{j})

tu calcules   \vec{i}  en fonction de  \vec{u} et  \vec{v}), idem pour   \vec{j}

tu poses \vec{OM} = X.\vec{u} + Y.\vec{v}   = x.\vec{i} + y.\vec{j} pour déterminer X et Y en fonction de x et y  

(tu reverras tes expressions de \vec{u}   et   \vec{v}  qui me semblent tous un peu)

Posté par
diracre : Déterminer l'équation d'un ensemble de points 03-01-21 à 18:08

Ah zut je viens de recroiser PLSUV que je salue bien ... et qui t'alerte également sur la rectitude de l'expression du vecteur

Posté par
diracre : Déterminer l'équation d'un ensemble de points 03-01-21 à 18:57

"Ah zut je viens de recroiser PLSUV ..."
On (un de mes enfants) me fait remarquer que le propos peut passer pour désobligeant ..
C'est en fait un condensé "Ah zut je n'ai pas vu que mon message croise celui posté par PLSUV il y a un instant"
ça fait plus de mots, mais c'es plus clair, merci Lucas

Posté par
PLSVUre : Déterminer l'équation d'un ensemble de points 03-01-21 à 19:08

Aucun problème .
Heureusement que tu as posté tes longs calculs....
(  autre méthode rotation de centre O et d"angle -π/6)
avec geogebra... puis avec les formules


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !