Inscription / Connexion Nouveau Sujet
Déterminer les réel a et b avec le point d'une courbe
Alors j'ai une fonction définie sur R\(3) qui est
h(x)= ax + b + 2
x-3
Et on me demande de trouver les réel a et b opur que la courbe de h passe par le point A(2;1) et que la tangente en ce point soir horizontale.
J'ai essayé de faire la technique habituelle de dévellopement ce qui me donne :
ax2-3ax+bx-3b+2
x-3
Mais aprés je ne vois pas du tout comment faire ... Est ce que j'ai pris la mauvaise direction ?
Si vous pouviez m'aider ce serait sympa =)
Bonjour
"la courbe de h passe par le point A(2;1)" donne h(2) = 1
"et que la tangente en ce point soir horizontale" donne h'(2) = 0
ce qui conduit à un système de deux équations à deux inconnues a et b

non c la bonne direction
et tu sais que la courbe passe par A(2,1) donc que f(2) =1
de plus la tengente en 2 est horzontal d'ou f'(2) = 0
tu donne f(2) en fonction de a et b et tu en déduis 1 en fonction de a et b
et tu donne f'(2) en fonction de a et b e tu en déduis 0 en fonction de a et b
et tu as un systeme de deux equations a deux equations a resoudre
bon courage
non en faite tu n'est pas obliger de transformer f en mettant sous le meme denominateur
c plus simple si tu garde f(x) = ax +b + 2: (x-3)
bon courage
Je ne suis vraiment pas sure d'avoir compris; ça donnerais donc :
h(2)=-2a-b+2=1
h'(2)=-2a-b+2=0 ?
Et aprés comment on fait pour trouver la valeur de a et de b du coup ?
non tu as h(2 ) = 2a +b + 2 : (-1) = 2a + b -2
donc 2a + b -2 = 1
tu as h'(x) = a - 2/(x-3)^2
donc h'(2) = a - 2/(-1)^2 = a -2
donc a-2= 0
a=2
donc 2*2+b -2 = 1 donc 2+b = 1 d'ou b = -1
voila bon courage
je pense qu'il y a une erreur.
La courbe passe au point A(2,1), donc h(2) = 1,, c'est la 1e équation.
On trouve 2a + b = 3.
Et la tangent de la courbe au point A est horizontale, donc h'(1) = 2.
h'(x) = a - 2/(x - 3)^2.
C'est la 2e équation.
On trouve a = 5/2.
Et b = -2.
Desole, je me suis trompe.
La tengent au point A est horizontale, donc h'(x) = 1.
h'(2) = 1.
En fin a = 3, b = -3.
Merci pour votre aide =)
Juste une question, si la tangente est horizontale pourquoi h'(x) n'est pas egale a 0 ?
> LoOo
si la tangente est horizontale pourquoi h'(x) n'est pas egale a 0 ?
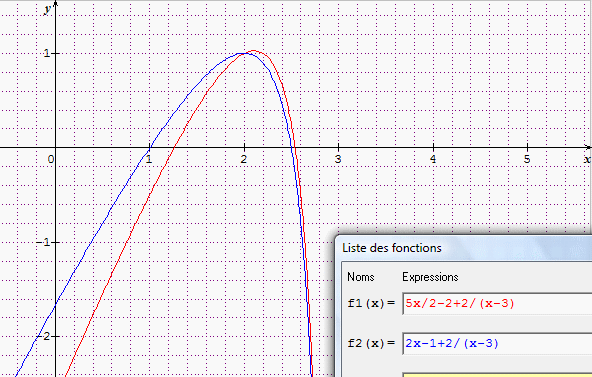
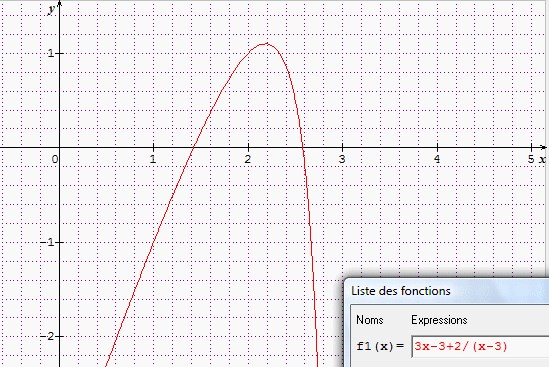
A toi de faire ton choix dans ce qui a été proposé (les graphiques peuvent t'aider)

Mais vu les graphiques, la solution c'est a=2 et b=-1 non ??? Parce qu'il faut que la tangente soit horizontale au point A
Je suis toute embrouillée ^^
je suis désolé littleguy mais il n'y a pas d'erreur dans ce que j'ai fait j'en suis sur
on a h(2)=1 et h'(2)= O ce qui conduit a a=2 et b=-1
> romscau Je n'ai pas dit le contraire. Les graphiques fournis étaient là pour montrer à thinhgt18 qu'il s'était trompé (j'ai mis sur le même graphique ta réponse et sa première réponse, puis sa deuxième proposition) 
Je me suis trompe, le graphique est très clair. Et Lolo, les résultats ou a=2 et b = -1, c'est bon. Vous avez des bons amis.
Litteguy et Romscau, vous êtes très intelligents.
J'ai enfin fini cet exercice et c'est grave a vous tous =D ! Et en plus de ça je suis sure de pouvoir le refaire en interro tellement il m'a marqué XD si c'est pas magique ça ...
Encore merci !!!