Inscription / Connexion Nouveau Sujet
Determiner les solutions de l'équation f(x)=0
Bonjour je n'arrive pas a faire sa : Déterminer les solutions de l'équation f(x)=0 sachant que l'équation de base est : 3x²-5x+1 . Merci a vous . 
Bonjour,
c'est la seule question ? aucune autre question avant en rapport avec cet éxo ?
qu'as tu vu en cours sur ces équations ?
en seconde en principe c'est "quasiment rien", d'où ma question sur des questions préliminaires d'où on peut tirer une résolution.
bien entendu cette équation est bien dans l'énoncé, écrite comme ça, et ce n'est pas un truc tiré d'un calcul précédent ... qui pourrait éventuellement être faux
Bonjour,
Il doit y avoir d'autres questions !!!
Du genre montrer que f(x) peut s'écrire sous la forme (...  ...) (....
...) (....  ... )
... )
tu as du voir la forme canonique en seconde, tu peux utiliser des formules ou bien refaire toute la démonstration :
3x2-5x+1=3(x2-5/3x+1/3)
3x2-5x+1=3((x-5/6)2-(5/6)2+1/3)
3x2-5x+1=3((x-5/6)2-25/36+1/3)
or -25/36+1/3=-25/36+12/36=(-25+12)/36=-13/36
d'où ;
3x2-5x+1=3((x-5/6)2-13/36)
3x2-5x+1=3(x-5/6)2-13/12
donc 3x2-5x+1=0
<=> 3(x-5/6)2-13/12=0
<=> (x-5/6)2=13/36
<=> x-5/6= (13/36) ou -
(13/36) ou - (13/36)
(13/36)
<=> x=5/6+ (13)/6 ou 5/6-
(13)/6 ou 5/6- (13)/6
(13)/6
Bonsoir,
En fait on te demande de résoudre l'équation du second degré 3x2-5x+1=0
Tu dois donc trouver x1et x2
Tu as certainement vu çà en cours
Enfaite j'ai eu plusieurs questions effectivement et l'énoncé est : On considère la fonction f définie sur l'intervalle [-2;4] par f(x) = 3x²-5x+1 .
1- Tracer la courbe représentative de la fonction f a l'aide de votre calculatrice ( Menu GRAPH) .
2- Régler la fenêtre de visualisation avec les valeurs ci - dessous :
(V-Windows)
Xmin= -2 Xmax=4 Scale = 1
Ymin= -5 Ymax=30 Scale = 1
Etc^^
hervelo .... mettre sous forme canonique = hors programme en seconde !
Pirho.... résoudre une équation du second degré = programme de 1ère pas de seconde !
Bone nut !
Et la prochaine fois, si tu veux de l'aide, tu postes correctement ton énoncé complet dans le bon forum !
on trouve pas exactement 0 vu que c'est des valeurs approchées des solutions, mais on doit trouver quelque chose proche de 0.
pour trouver exactement 0 utilise les valeurs exactes :
(5+ (13)/6 ou (5-
(13)/6 ou (5- (13)/6
(13)/6
Tu n'as donc rien compris à nos conseils !
Il n'y a qu'une et une seule question ?
Tu dis que maintenant , il y a un graphique ! Il n'y aurait pas autre chose ?
Pour t'aider, il nous faut tous les indices !!! On ne va pas deviner ce que tu as sous les yeux et que tu ne nous dis pas ! Grrrrr !
Mon graphique contient
x , -2 , -1.5 , -1 , -0.5 , 0 , 1 , 1.5 , 2 , 2.5 , 3 , 3.5 , 4.
f(x), 23 , 15.25 , 9 , 4.25 , 1 , -0.75 , -1 , 0.25 , 3 , 7.25 , 13 , 20.25 , 29
Et la seule et unique question en seconde en France est :
En ayant comme information(s) .... les quelles ??? on ne sait toujours pas ....
Déterminer les solutions de l'équation f(x)=0
Je suis désolé mais tout ce qu'il y'a c'est ce que je vous est dit : Le tableau avec les f(x) et les x et Xmin = -2 Xmax= 4 , Ymin = -5 et Ymax = 30
ton problème demande de faire une résolution graphique.
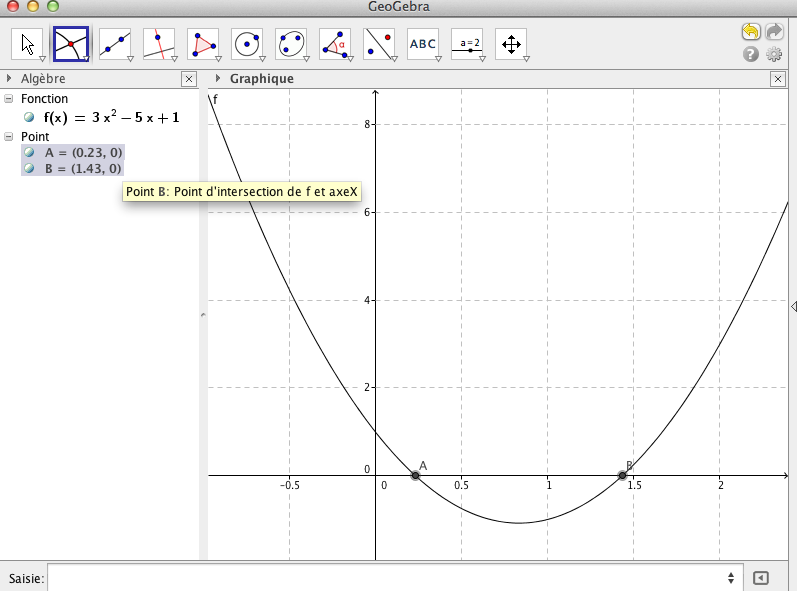
vu le tableau des valeurs, on peut dire que la première solution est entre 0 et 0,5 ; et la seconde entre 1 et 1,5.
en traçant la courbe, on doit pouvoir lire sur le graphique que les solutions sont environ 0,2 et 1,4.
inutile de donner plus de précision à ce niveau.