Inscription / Connexion Nouveau Sujet
Déterminer un déplacement.
Bonjour ,
Merci d'avance. 
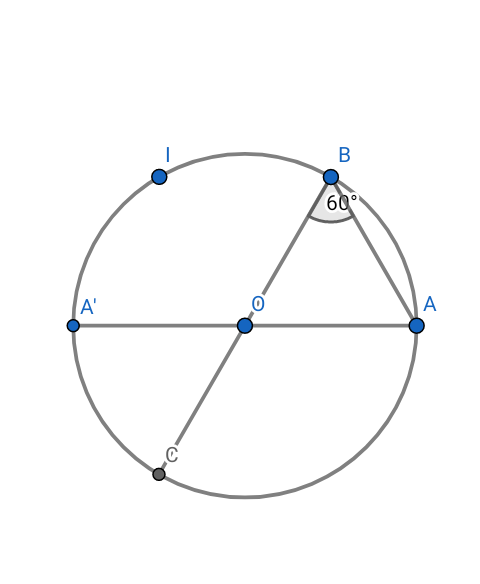
Soit (C) un cercle de centre O et de diamètre [BC]. A le point de (C) tel que .
A' le point diamétralement opposée à A sur (C) et .
1) Démontrer qu'il existe un unique déplacement f tel que f(A)=C et f(B)=O.
2) Démontrer que f est une rotation dont on précisera l'angle.
3) Démontrer que est le centre de f.
Réponses
1) .
Je ne vois pas vraiment le lien avec un déplacement.. 
Bonjour
Il faut rectifier la figure. Inverser A et I.
Un déplacement du plan est soit une rotation, soit une translation. Par théorème
, il existe un unique déplacement f tel que f(A) = A' et f(B ) = B' SSI AB= A'B'. Comme f(A) = C et
f (B) =O, Il faut vérifier que....?????
Tout déplacement est soit une translation si vect (AB) = vect (A'B') soit une rotation d'angle (vect(AB),vect(A'B')). Cela permet de répondre à la question 2.
Pour la question 3, on peut par ex montrer que I est sur les médiatrices de [CA] et[BO].
Autre stratégie, définir un repère de centre O , tel que le cercle soit de rayon 1 et (BC) l'axe des abscisses. Et utiliser les nombres complexes. Un déplacement a pour écriture z' = az +b, avec |a|=1....
breuil, bonjour et bienvenue
Merci de prendre connaissance de ![]() Sujet ancien- ne plus donner ce lien-merci
Sujet ancien- ne plus donner ce lien-merci
matheux14 n'avait pas encore eu le temps de revenir sur son exo, donc une nouvelle intervention n'était peut-être pas indispensable...mais bon, je pense que tous les nouveaux inscrits ont besoin de faire leurs premiers pas
Bonne découverte en tout cas

Bonjour ,
1) Le triangle OAB est équilatéral.
Donc AB=OB.
B étant diamétralement opposé à C , on a OA=OC.
==> AB=OC avec A ≠ C.
Donc il existe un unique déplacement f tel que f(A)=C et f(B)=O.
2) OAB est un triangle et B et C sont diamétralement opposés.
Donc et
ne sont pas colinéaires.
Il vient .
Par conséquent f est une rotation d'angle .
3)
*
f
------
A | C
B | O
Le centre de f est le point d'intersection des médiatrices de [AC] et [BO].
*
S(BC)
--------
O | O
B | B
A | I
OBI , l'image de OBA par S(BC) est un triangle équilatéral.
Donc IO=IB donc I appartient à la médiatrice de [OB].
*
S(BC)
----------
[ A | I ]
[ C | C ]
B | B
L'angle (ICB) est l'image de l'angle (ACB) par S(BC).
Donc mes (ICB)= mes (ACB)= .
mes (ACI) = mes(ACB) + mes(BCI)=.
Comme CA=CI alors ACI est équilatéral. Donc IC=IA.
I appartient donc à la médiatrice de [AC].
Le centre de f est donc le point I.
breuil j'ai pas compris l'autre stratégie.. C'est quoi l'intérêt ?


