Inscription / Connexion Nouveau Sujet
Déterminer un encadrement
Bonsoir à tous les membres du groupe.
J'ai un exercice qui cause un peu de soucis
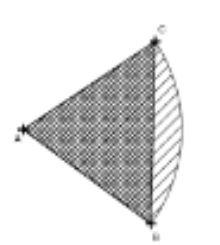
Énoncé :la figure ci-contre représente une position d'un disque de centre A et de rayon 1. On fait varier la mesure en radian de l'angle BAC dans l'intervalle]0,π].
Question : déterminer un encadrement d'amplitude 10^-3 d'une mesure de l'angle BAC pour laquelle il y'a égalité des aires de la surface hachurée et de la surface quadrillée.
La première idée est l'aire d'un triangle qui base x hauteur divisé par 2 et l'air d'un disque qui est πxR^2(coe R=1) , donc S(d)=π
ABC est un triangle équilatéral circonscrit à un disque de centre A et de rayon 1.
J'ai des difficulté à schématiser par le logiciel en ligne.
Bonsoir,
Sans la figure qui est jointe à l'exercice, difficile d'aider.
On fait varier la mesure en radian de l'angle BAC
Et comment savoir ce qui est hachuré ou quadrillé ?
Le bouton "Img" sous la zone de saisie permet de joindre une image.
Vous avez la figure sur votre énoncé. Vous pouvez la scanner et l'envoyer
voir FAQ question 05
Surface hachurée ? quadrillée ?
Que vaut CB ?
Appelez par exemple I son milieu
En utilisant les relations trigonométriques calculez CI
puis AI enfin l'aire du triangle ABC
Aire du secteur angulaire est
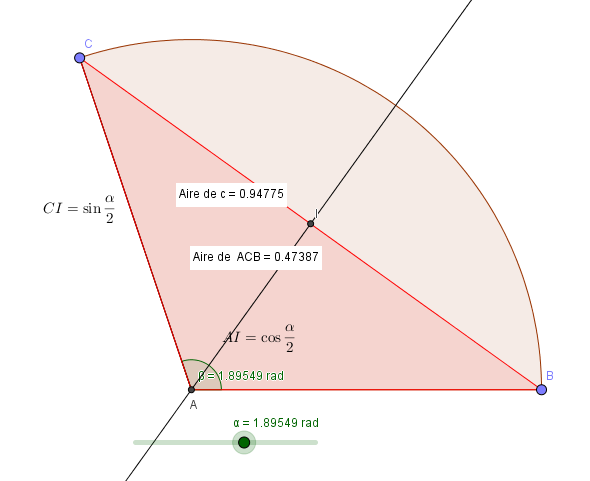
La partie quadrillée est bien le triangle ABC.
Pour calculer l'aire on a besoin de BC et de AI, c'est-à-dire la longueur de la hauteur correspondante
AIB ou ACI sont des triangles rectangles on peut donc utiliser la trigonométrie vue en 3e
On sait aussi que
Quelle est l'aire du triangle ABC ?
Il est bien entendu qu'ABC est un triangle isocèle donc la hauteur issue du sommet principal est aussi médiane médiatrice bissectrice par conséquent l'angle en A dans le triangle ABI vaut bien la moitié de l'angle en A dans le triangle ABC
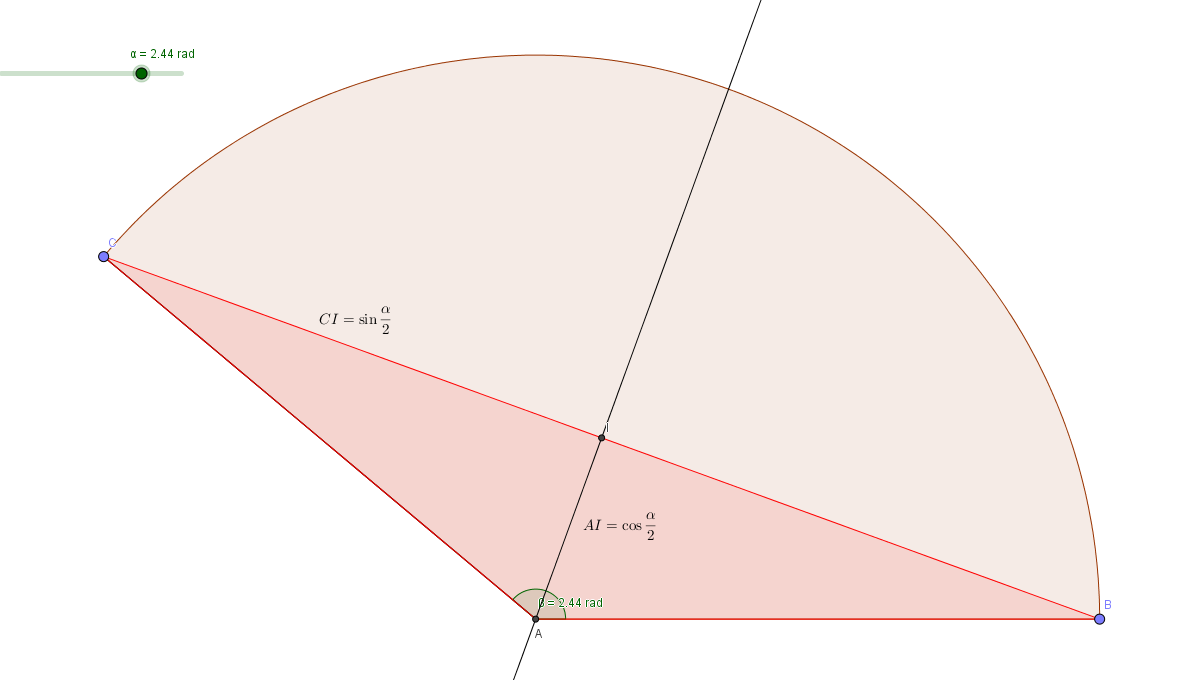
Vous avez calculé l'aire du triangle en rouge sur la figure l'aire du secteur angulaire
Pour qu'il y ait égalité on devra avoir l'aire du triangle = l'aire de la partie en brun ici, c'est-à-dire la moitié du secteur circulaire.
Je vous ai donné des indications donc c'est à vous maintenant de proposer une solution.
Ici, on ne traite pas les problèmes à votre place.
Comme j'ai exprimer ABC en fonction de sinÂcos qu'est ce que je dois faire par après.
J'ai un peu de mal à trouver sur le schéma guide-moi et je vais m'en sortir.
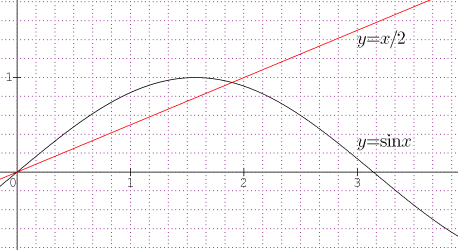
D'accord,maintenant pour montrer l'égalité je dois prendre l'aire de la partie angulaire Alpha/2 - sin(2Tete)=sinÂcosÂ.
Où bien comment.
Merci d'avance
L'objectif c'est de donner un encadrement à 10^-3
Aire du triangle=1/2 air de secteur angulaire est que je peux trouver l'encadrement.
Merci.