Inscription / Connexion Nouveau Sujet
devoir de maths (triangle, racines carrés) PT.2
Bonjour, voici la deuxième partie de mon DM:
5-Ecrire 11 sous la forme d'une somme de trois carrés parfaits.
Combien de triangles suffit-il de construire pour tracer un segment de longueur de racine carré de 11?
6-Le mathématicien Joseph Louis Lagrange (1736-1813) a démontré que tout entier positif peut s'écrire sous la forme de la somme d'au plus quatre carrés parfaits.
a) Combien de triangles rectangles peuvent suffire pour construire un segment de longueur racine carré de n?
b) En remarquant que 75=8²+3²+1²+1², construire un segment de longueur de racine carré 75 en traçant successivement trois triangles rectangles.
Je comprends le sens des carrés parfaits, mais l'interpréter, j'ai du mal...
Je n'ai pas compris la a)... Pouvez vous m'éclairer???
Bonjour,
oui et ... ?
Ecrire 11 sous la forme d'une somme de trois carrés parfaits
quels carrés trouves tu dont la somme fait 11 ?
ensuite le principe c'est ça
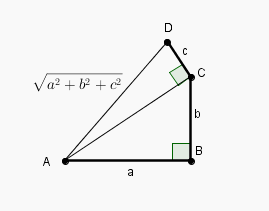
si n = a² + b² + c² est une somme de (ici 3) carrés
en construisant deux (ici) triangles rectangles, on construit
preuve par Pythagore.
donc si on a une somme de 3 carrés, avec 2 triangles rectangles
si on a une somme de 4 carrés combien faut il de triangles rectangles ?
tout est dit
tu n'as plus qu'à appliquer ça aux exemples numériques de ton énoncé.
D'accord, en réflechissant avec un ami, j'ai pu trouver les premières questions.
Mais je ne comprends pas ta phrase
si n = a² + b² + c² est une somme de (ici 3) carrés
en construisant deux (ici) triangles rectangles, on construit \sqrt{n}
preuve par Pythagore.
as tu au moins vu la figure correspondante ?
et calculé Pythagore dans les deux triangles rectangles ?
le "ici" c'est tout simplement que cette figure est (forcément) dans un cas particulier !
et que si j'ai une somme de disons 5 carrés, il me faudra 4 triangles rectangles successifs. etc etc ...
et à l'inverse si j'ai une somme de seulement deux carrés, un seul triangle rectangle suffit.
Les carrés sont bien:3²+1²+1²?
Pour les 4 carrés, il faudra 3 triangles et là, je continue la figure, c'est bon?
Oui, j'ai compris tout ça mathafou, mon problème, c'est comment... l'exprimer.
Et là, la citation que j'ai relevé qui, en l'occurence concerne ta phrase sur , eh bien je ne la comprends! Le "preuve de Pythagore" me chiffone!
Toutefois, j'ai remarqué que il faut 3 carrés pour 2 triangles, 4 pour 3 etc..
Pythagore dans ABC : AC² = AB² + BC² = a² + b²
Pythagore dans ACD : AD² = AC² + CD² = (a² + b²) + c²
mais sans doute cherchais tu midi à 14 heures et plus compliqué que ça ??
il faut 3 carrés pour 2 triangles, 4 pour 3 etc..
on donne n et on cherche à construire
n
donc on décompose n en somme de carrés (de nombres) et on n'a pas trop le choix, c'est la valeur de n qui impose le nombre de carrés !
et de ce nombre de carrés (de nombres carrés) on en déduit le nombre de triangles nécessaire pour la construction géométrique de la longueur
n
l'énoncé est d'ailleurs mal foutu :
Combien de triangles rectangles peuvent suffire pour construire un segment de longueur racine carré de n
si n est un carré, construire sa racine carrée ne nécessite aucun triangle. il suffit donc de ne tracer aucun triangle !
donc il peut suffire (parfois) de 0 triangle.
ce n'est certainement pas le sens que celui qui a rédigé cet énoncé voulait donner à sa phrase !!
il voulait dire : combien au maximum de triangles peuvent suffire à ...
comme un nombre est somme de 4 carrés au maximum, etc ...
Du coup, je peux répondre: Selon racine carré de n, le nombre de carrés sera inférieur de racine carré de n de 1.
C'est une bonne réponse pour la question a)?
c'est une expression pour dire : tu cherches des complications où il n'y en a pas.
tiens au passage l'exemple de 75 de l'énoncé et bien mal choisi car
75 = 7² + 5² + 1²
= 5² + 5² + 5²
= 8² + 3² + 1² + 1²
= 7² + 4² + 3² + 1²
= 5² + 5² + 4² + 3²
alors certes 75 est somme de 4 carrés, mais il suffit de prendre 3 carrés et donc avec deux triangles seulement on peut construire 75.
(par exemple à partir de l'assez évident 75 = 5² + 5² + 5²)
et même un seul !! (avec une autre méthode 75 = 10² - 5²)
je me suis laissé dire que 7, 15 et 23 sont les seuls nombres qui nécessitent 4 carrés de façon unique
les autres nombres qui nécessitent 4 carrés donnent de (très) nombreuses variantes, comme le 75 de l'énoncé qui se décompose en 4 carrés non nuls de trois façons différentes.
Mais tout ceci est un peu "au dela de l'énoncé", juste pour la curiosité.
l'énoncé demande juste avec 75 écrit comme somme de ces 4 carrés donnés et pas de construire 75 de la façon la plus économique possible !
Bon, d'accord. Je peux dire que le nombre de triangles dépendra de racine carré de n? (ma prof est très stricte côté rédaction...)
Selon racine carré de n, le nombre de carrés sera inférieur de racine carré de n de 1.
non.
cela n'a aucun raport avec la valeur de la racine carrée de n.
mais uniquement avec le nombre de carrés nécessaires pour écrire n sous forme de somme de 4 carrés
Lagrange affirme que quel que soit n on peut toujours écrire n sous forme de somme de 4 carrés au maximum
donc on peut toujours construire
n avec au maximum 3 triangles rectangles (= 4-1)
et "parfois" avec moins
déterminer combien de carrés (non nuls) sont nécessaires pour décomposer n en somme de carrés ne se fait pas directement sur la valeur de n
il faut utiliser des abominations du genre décomposition de n en nombres premiers etc ...
Mais n est inconnu! Il peut être n'importe quels nombres! Le nombre de triangles peut très bien être 5,7,10...
Qu'est ce que vous mettriez vous donc comme phrase???
posts croisés ou c'est en réponse à celui (23:27) qui expliquait que 3 triangles suffisent toujours ? et ce quel que soit n
Lagrange affirme que quel que soit n on peut toujours écrire n sous forme de somme de 4 carrés au maximum
donc on peut toujours construire
n avec au maximum 3 triangles rectangles (= 4-1)
Annuler
connectez vous