Inscription / Connexion Nouveau Sujet
Devoir maison algorithme
Voila mon prof de math me demander de trouver un algorithme qui trouverai l'angle entre les heures et les minutes, voici le sujet
Ce devoir consiste à écrire un algorithme qui prends deux nombres entiers
en entrée qui donnent l'heure au format classique français. Par exemple
19 et 57 pour 19H57.
La sortie de l'algorithme doit donner l'angle qu'auraient les deux aiguilles,
des heures et des minutes, si l'heure était affichée sur une horloge classique
à aiguilles.
L'angle donné doit être en degrés et correspondre à l'angle saillant, c'est
à dire être entre 0 et 180.
Par exemple si un utilisateur saisit 6 et 35 l'algorithme doit répondre 30.
Il est fortement recommandé d'installer EduPython et de tester la version
programmée de votre algorithme pour vérifier qu'il marche et que
vous n'avez pas oublié de cas fâcheux.
Malheureusement je ne comprend rien j'ai deja essayer plusieurs techniques pour trouver l'angle de 6 et 35 mais je ne tombe jamais sur 30 et j'arrive encore moins a trouver l'algorithme.... pourriez vous m'aidez svp... j'aimerais que vous me donneriez la solution en me décrivant le calcul et l'algorithme afin de les comprendres et comprendre ce que j'écris.
Rezol77340
Bonsoir,
Soient les paramètres et
correspondants à l'heure et aux minutes; et
leurs angles respectifs par rapport à position
. Quelles relations les lient?
Bonjour,
6 et 35 l'algorithme doit répondre 30
malheureusement c'est faux ... c'est 12,5 degrés ...
(car pendant les 35 minutes, la petite aiguille a avancé et n'est pus sur le 6h)
Bonsoir,
Si l'utilisateur saisit 6 puis 35, l'angle ne peut être 30°
Car en 35 minutes la petite aiguille a avancé entre le chiffre 6 et le chiffre 7 de 35/60 des 30°. L'angle des 2 aiguilles est donc de 30x(25/60)°
@ mathafou : à cette heure tardive, je n'ai pas vérifié que mon intervention allait venir après la votre.
Mais voilà pour vous une occasion d'un algorithme codé en Pyhon 
il 60 divisions dans le cadran. 6h00 se trouve à la division 30. Et 35mn se trouve à la division 35. Donc l'angle entre les deux correspond à 5 divisions qui correspond en degré à 5*360/60=30°
je n'ai jamais vu aucune montre ni pendule à aiguilles, qu'elles soient à quartz ou pas, qui fait sauter brusquement la petite aiguille de 30° d'un coup au passage d'une heure à l'autre 
Moi non plus.
Maintenant, soit on fait avec soit on attends une réponse de Rezol77340 (qui a mon avis n'a pas cette réponse).
Bonjour.
Ma proposition en Python :
#*******************************************************************************
# IMPORT ***********************************************************************
#*******************************************************************************
# module pour le système d'exploitation
import os
# module specifique pour le systeme
import sys
# module pour les expressions regulieres
import re
#*******************************************************************************
# MAIN *************************************************************************
#*******************************************************************************
# effacement de l'ecran
os.system('cls')
print "\n"
while 1 :
# entrees possibles
# - heure sous le format hh.mm, 00 < hh < 24, 00 <= mm < 60
# - 'q' pour quitter
entree = raw_input("\n Entrer l'heure sous la forme hh.mm (de 00.00 a 23.59) ou q pour quitter : ")
print "\n"
# entree "q" ?
match = re.match("q", entree)
if match :
# arret du script
sys.exit()
# entree "hh.mm" ?
match = re.match("(\d{1,2})\.(\d{1,2})", entree)
if match :
# recuperation des heures au format int
hh = int(match.group(1))
# recuperation des minutes au format int
mm = int(match.group(2))
# test de validite des heures et des minutes
if hh < 24 and mm < 60 :
if hh >= 12 :
hh -= 12
# calcul de l'angle de l'aiguille des minutes
angle_mm = 6.0 * mm
# calcul de l'angle de l'aiguille des heures
angle_hh = (60 * hh + mm) / 2.0
# angle entre les aiguilles
angle = abs(angle_hh - angle_mm)
# angle aigu ?
if angle > 180 :
angle = 360 - angle
print " %02d:%02d angle = % 3.1f deg.\n" % (hh, mm, angle)
imports, expressions régulières etc sont bien au dela de ce qu'on attend en seconde !!
à mon avis on attend uniquement
def angle(h, m):
# calcul
return l'angle calculé
et c'est tout.
et en tapant angle(6,35)
cela doit retourner (et donc afficher) 12.5
(ou 30° avec la pendule farfelue du prof  )
)
Bonjour,
très bien bbomaths. programme (algorithme) bien documenté
sauf pour le while 1: qui risque de poser une question de compréhension...
et pour une petite aiguille qui ne saute pas brutalement d'heure en heure (voir Razes)
Tourne OK si on met des parenthèses aux print (depuis la version 3)
et sous idle mettre input simple au lieu de raw_input
hh et mm pourraient être entrés successivement pour ne pas avoir à traiter hh.mm comme expression régulière
Bonjour,
en Python, connaitre import est indispensable
dès que l'on fait des calculs. Sont nécessaires par exemple :
from math import sqrt
import time
par contre, import os ou import sys sont en général implicites
entierement d'accord avec mathafou
il ne faut pas oublier que les eleves de seconde decouvrent python
ils vont travailler avec Edupython
je doute que le niveau requis de connaissance du Python en seconde soit aussi étendu que cela !!
(et même en Terminale "niveau bac" d'ailleurs)
la seule chose que ça risque de produire est de perdre complètement le demandeur.
écrire une fonction toute nue qui calcule ce qu'on demande de calculer et uniquement et c'est tout.
(et aucun besoin d'import de quoi que ce soit, ni de math ni de time, pour faire ça)
Il faut bien exécuter ce qui est écrit en python sinon,
"écrire une fonction toute nue" que l'on ne fait pas s'exécuter manque de rigueur.
pfff
et en tapant angle(6,35)
cela doit retourner (et donc afficher) 12.5
il ne s'agit pas de faire des cours de programmation en Python
mais d'utiliser Python pour illustrer des cours d'algorithmique !
cela a toujours été le seul et unique objectif des cours d'algorithmique en Lycée en classes de mathématiques
il n'y a pas de cours d'informatique au lycée.
que la réponse demandée soit
un algorithme en langage dit naturel
ou en Algobox
ou sur calculette
ou dorénavant en Python
ou en Python "trafiqué" (langage naturel "à la mode Python" hybridé avec des conventions de calculette)
et rien d'autre
pas de faire des modules Python complets autonomes disant papa maman et faisant le café...
mais comme Rezol77340 s'est complètement désintéressé de la question pour l'instant ...
quand il reviendra il sera complètement largué de chez largué avec toutes ces digressions et hors sujet
le sujet c'est savoir décrire "algorithmiquement" un calcul à partir d'une analyse mathématique du problème
et comprendre les structures conditionnelles "si" ("if") et la syntaxe de base du langage Python pour écrire cet algorithme
et c'est tout.
pas les notions de main, input, print, etc qui feraient un programme Python entier autonome
Je répète donc : Un algorithme que l'on ne traduit pas en "exécutable", c'est du n'importe quoi.
tant chacun a expérimenté les erreurs que l'on fait, visibles ou cachées.
Jai regardé la documentation de mise en oeuvre de EduPython,
en https://download.tuxfamily.org/edupython/EduPython1.0.pdf
Le premier affichage du premier écran de zone affichage montre, pour débuter :
from lycee import *
print "Hello world"
et même sans "from lycee import *" du tout (ça c'est juste pour franciser Python et importer automatiquement quelques trucs par défaut)
en tapant directement et uniquement (par exemple)
def angle(h,m):
if h>=12 :
h=h-12
angle_heures = (h+m/60)*360/12
angle_min = m*360/60
angle_aiguilles = angle_heures-angle_min
if angle_aiguilles < 0 :
angle_aiguilles = -angle_aiguilles
if angle_aiguilles > 180:
angle_aiguilles = 360-angle_aiguilles
return angle_aiguilles
et dans la console : angle(6,35)
dans la console apparait le résultat : 12.5
point barre et c'est tout ce qu'on demande ici
(évidemment l'algorithme lui-même peut être différent de celui que j'ai écrit, c'est le but de cet exo de définir un calcul qui marche et de l'écrire sous forme d'un algorithme qui marche, chacun peut calculer ça différemment)
bonjour,
je ne comprend pas comment faut il faire quelqu'un pourrait m'expliquer le plus simplement possible.
Merci d'avance bonne journée.
1ere étape :
analyse mathématique du problème, angle des aiguilles en fonction du temps
étudier les différents cas de figure
2ème étape :
en déduire les opérations précises à effectuer pour obtenir le résultat demandé
3ème étape :
coder l'enchainement de ces opérations avec un langage de son choix, et l'énoncé dit "en Python"
(donc connaitre la syntaxe de base de Python)
Jai regardé la documentation de mise en oeuvre de EduPython,
autant installer Edupython
1/ ecrire la fonction dans la fenetre d'edition
2/ appuyer sur le bouton Exécuter
3/ faire des appels de la fonction dans la console
certainement pas, ton calcul ne rime à rien du tout.
quand on dit qu'il est 6:35 cela veut dire 6 heures et 35 minutes pas 6/35 
calculer la position de la petite aiguille à 6h35 (de façon générale à l'heure h heures et m minutes) sachant que en 12h elle fait un tour complet = 360°
calculer la position de la grande aiguille à 6h35 (de façon générale à h:m) sachant que en 60 minutes elle fait un tour complet
faire la différence des deux angles, "dans le bon sens" et "comme il faut" pour avoir "l'angle saillant" (c'est à dire entre 0 et 180°) entre les positions de l'aiguille des heures et de l'aiguille des minutes.
ahhh d'accord je n'avais pas compris sa comme tel.
merci beaucoup de ces réponses très rapide et bonne journée .
Bonjour.
Quelqu'un peut-il m'expliquer l'utilité de EduPython par rapport à Python (2.7 ou 3.3) ?
Pourquoi apprendre une version édulcorée (?) partiellement francisée et, surtout, inexistante dans le monde des employeurs ?
Par exemple, qu'apporte la fonction demande() alors qu'il existe une fonction native input() ?
Comment va se comporter un élève qui va se retrouver devant un bout de code de plus de 10 lignes en Python où la première ligne n'est pas "from lycee import *" ?
Quelle sera sa réaction lorsqu'il s'apercevra que dans tous les exemples qu'il trouvera sur le Net aucun ne comporte aucune des instructions francisées ?
comme je le disais (et en plus j'ai insisté lourdement) il est inutile de mettre le "from lycee"
et alors on a du vrai Python dans une console Python qui fait du pur Python "en live"
et pas en compilant un fichier Python pour obtenir de l'exécutable "indépendant"
les lycéens ont pour seul but de faire une initiation aux algorithmes
pas du tout de faire de la programmation en quelque langage que ce soit
cela concernera leurs cours d'informatique ultérieurs (pas de maths), selon leurs spécialisation et alors ils étudieront les spécificités complètes du langage Python (ou d'autres)
toute cette discussion n'a d'ailleurs rigoureusement rien à faire là (dans un sujet d'aide à un exercice !!)
au pire tous ces a-côtés, si intéressants soient-ils, seraient à mettre dans ![]() amenagements algorithmes
amenagements algorithmes
mettre tout ça ici ne fait que noyer les élèves qui demandent de l'aide sur cet exo
Bonjour,
Je suis du même avis que mathafou, j'ai toujours conseillé l'algorithmique avant de commencer à utiliser tel ou tel langage, car l'algorithme est le passage obligé pour élaborer une application.
De ce fait, j'ai toujours conseillé l'utilisation d'Algobox, car c'est un outil pédagogique très intéressant, très proche du langage naturel, léger et de plus gratuit. Passé ce stade, l'élève est outillé pour aborder facilement un langage de programmation.
J'ai jeté un coup d'œil à Edupython que je ne connaissait pas, j'ai trouvé qu'il ressemble aux langages ,
et au
. Les langages changent mais l'algorithmique non ou peu.
De ce fait, j'ai toujours conseillé l'utilisation d'Algobox, car c'est un outil pédagogique très intéressant, très proche du langage naturel, léger et de plus gratuit. Passé ce stade, l'élève est outillé pour aborder facilement un langage de programmation.
Justement pas.
Ce n'est pas moi qui le dit mais les enseignants d'informatique.
Bonjour.
2eme mouture (sous Python 2.7) avec une fonction calculer_angle()
#*******************************************************************************
# IMPORT ***********************************************************************
#*******************************************************************************
# module pour le système d'exploitation
import os
# module specifique pour le systeme
import sys
# module pour les expressions regulieres
import re
#******************************************************************************
# DEF *************************************************************************
#******************************************************************************
# -- calculer_angle -----------------------------------------------------------
#
# Description : calcul de l'angle aigu entre les 2 aiguilles d'une horloge ou
# d'une montre.
#
# Parameters : - arg_hh ~ heures de 0...23 (format int)
# - arg_mm ~ minutes de 0...59 (format int)
#
# Return : - angle calcule (format float)
#
# Notes : calculs :
#
# - aiguille des minutes : 1 tour ~ 360° ~ 60 min
# - aiguille des heures : 1/12 tour ~ 30° ~ 60 min
#
def calculer_angle(arg_hh, arg_mm) :
# heures modulo 12
if arg_hh >= 12 :
arg_hh -= 12
# calcul de l'angle de l'aiguille des minutes
angle_mm = 6.0 * arg_mm
# calcul de l'angle de l'aiguille des heures
angle_hh = (60.0 * arg_hh + arg_mm) / 2.0
# angle entre les aiguilles
angle = abs(angle_hh - angle_mm)
# angle aigu ?
if angle > 180.0 :
angle = 360.0 - angle
# donnee(s) retournee(s)
return angle
#*******************************************************************************
# MAIN *************************************************************************
#*******************************************************************************
# effacement de l'ecran
os.system('cls')
# boucle infinie
while 1 :
# entrees possibles
# - heure sous le format hh.mm avec 00 <= hh < 24, 00 <= mm < 60
# - 'q' pour quitter
entree = raw_input("\n Entrer l'heure sous la forme hh.mm (de 00.00 a 23.59) ou q pour quitter : ")
print "\n"
# entree "q" ?
match = re.match("q", entree)
if match :
# oui : arret du script
sys.exit()
# entree au format demande "hh.mm" ?
match = re.match("(\d{1,2})\.(\d{1,2})", entree)
if match :
# oui : recuperation des heures hh au format entier (int)
hh = int(match.group(1))
# recuperation des minutes mm au format entier (int)
mm = int(match.group(2))
# test de validite des heures (0 <= hh < 24) et des minutes (0 <= mm < 60)
if hh < 24 and mm < 60 :
# calcul de l'angle aigu
angle_aigu = calculer_angle(hh, mm)
# affichage
print " %02d:%02d angle = % 3.1f deg.\n" % (hh, mm, angle_aigu)
Exécution :
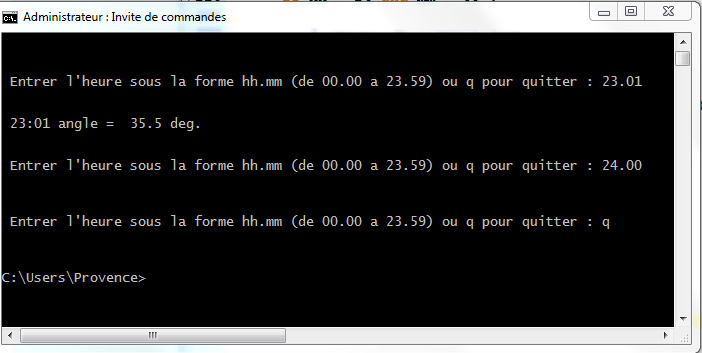
fonction calculer_angle() pouvant être utilisée seule... la même sans lignes blanches et sans commentaires :
def calculer_angle(arg_hh, arg_mm) :
if arg_hh >= 12 :
arg_hh -= 12
angle_mm = 6.0 * arg_mm
angle_hh = (60.0 * arg_hh + arg_mm) / 2.0
angle = abs(angle_hh - angle_mm)
if angle > 180.0 :
angle = 360.0 - angle
return angle
Exécution :
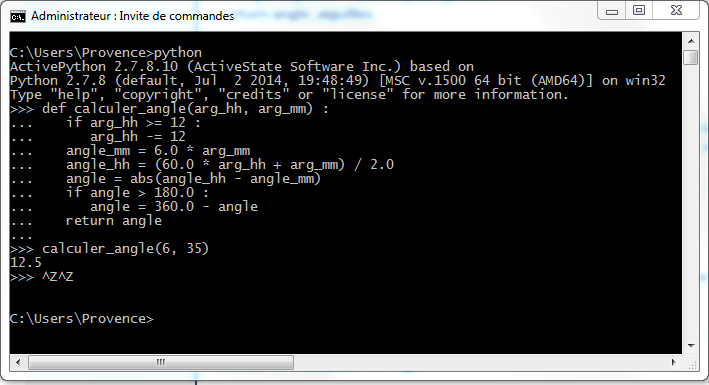
c'est pas croyable !!!
ce truc est certes très bien mais n'a AUCUN RAPPORT avec ce qui est demandé à un élève de SECONDE !!!
pffff
salut
testé avec vba ( bien que cela ne soit pas en rapport )
sub calcul_angle()
A = InputBox("saisir l'heure")
B = InputBox("saisir les minutes")
k1 = (6 * ((A Mod 12) * 60 + B)) Mod 360
k2 = (1 / 2) * ((A Mod 12) * 60 + B)
If Abs(k1 - k2) < 180 Then
MsgBox Abs(k1 - k2)
Else
MsgBox 360 - Abs(k1 - k2) ' retourne l'ecart entre les deux aiguilles
End If
pour 6h35 l'angle est de 12,5°
le choix est tout vu compte tenu des consignes explicites de l'énoncé et du niveau seconde
Il est fortement recommandé d'installer EduPython et de tester la version
programmée de votre algorithme pour vérifier qu'il marche et que
vous n'avez pas oublié de cas fâcheux.
et
si un utilisateur saisit 6 et 35
Bonsoir.
Juste pour info, il suffit de modifier 2 lignes de mon script pour une saisie des entrées sous la forme "hh,mm" ou "hh mm".
La ligne :
entree = raw_input("\n Entrer l'heure sous la forme hh.mm (de 00.00 a 23.59) ou q pour quitter : ")
devient :
entree = raw_input("\n Entrer l'heure sous la forme hh mm ou hh,mm (de 00:00 a 23:59) ou q pour quitter : ")
La ligne :
match = re.match("(\d{1,2})\.(\d{1,2})", entree)
devient :
match = re.match("(\d{1,2})[\.\s,](\d{1,2})", entree)
Ce qui donne à l'exécution :
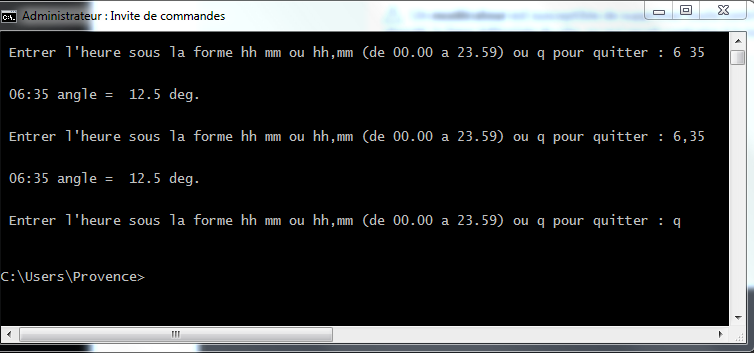
Remarque : le script (100% python 2.7) est proposé comme piste et peut être modifié, porté vers Python 3.3 et, utilisé par d'autres librairies.
@tous
lorsque les reponses ne sont pas adaptees au niveau du posteur,
il serait preferable d'ouvrir un topic dans le forum Espace Profs.
D'autant plus que ce qui vient d'etre ecrit pourraient interesser tous les enseigants,
la plupart ne connaissant pas python.
Merci énormément de votre soutien, j'ai réussi a faire mon propre programme sur ma calculette et j'en suis très heureux car ce sont de longues heures passer dessus. pouvez vous me donnez votre avis pour savoir ce que je pourrai enlevé pour diminuer/compacter au maximum cet algorithme, et encore merci a TOUS
if A < 12
alors A-12 sera négatif !!!
ça ne semble pas bien malin !!
de toute façon puisque maintenant on sait que A est forcément < 0, tester A > 24 n'a aucun sens
je me suis arrêté là
avant de faire un programme
il faut élaborer (en français) la succession des opérations à effectuer
c'est ce qu'on appelle un algorithme (algorithme = la méthode exacte de calcul et rien d'autre que l'enchainement et la description de cette méthode)
donc le début de l'algorithme pourrait être (écrit exactement comme çà et rien d'autre)
comparer l'heure saisie à 12 (et éventuellement à 0 et 24)
et ensuite faire des actions cohérentes avec ça !
etc
ensuite seulement, une fois que cette description de méthode sera parfaitement claire, complète, et marchera (de façon abstraite) sur divers exemples que l'on peut imaginer pour la mettre en défaut,
seulement ensuite on le traduira dans le langage qu'on veut
sur ta calculette,
ou sur EduPython, (sans tenir compte des délires de certains qui voudraient te faire sauter deux classes)
écris en français les opérations que tu ferais à la main pour résoudre le problème de trouver l'angle des aiguilles en fonction de l'heure h et des minutes m
écris le EN FRANCAIS
toi tu dis que si h est < 12 il faut remplacer h par h-12
exemple h = 6, c'est < 12, je remplace h par 6-12 = -6 ... à quoi ça sert et qu'est ce donc que ça va donner de faire comme ça ?????
c'est complètement absurde.
après on verra pour faire un algorithme en machine mais tant que la méthode de calcul détaillée décrite en français des opérations à effectuer et pourquoi on les effectue n'est pas claire c'est totalement inutile de chercher à écrire du code.
Bonjour.
On reprend...
La première étape consiste à trouver les formules mathématiques qui donnent les différents angles utiles.
L'aiguille des minutes fait un tour de quadrant (360°) en 60 min. On peut donc calculer sa vitesse de rotation :
°/min
L'aiguille des heures fait un tour de quadrant (360°) en 12 x 60 min = 720 min. On peut donc calculer sa vitesse de rotation :
°/min