Inscription / Connexion Nouveau Sujet
Difficulté sur un DM partie 2
Le mathématicien arabe al-Khuwarizmi (IX° siècle)cherchait la longueur x telle que l'aire du rectangle AEFD ci-dessous soit égale à 21.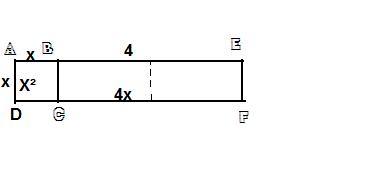
1/a) Ecrire l'aire du rectangle AEFD en fonction de x.
b) En déduire l'équation que doit vérifier x pour répondre au problême.
2/Soit les fonctions f et g définies par IR par :
f(x) = x² g(x) = -4x + 21
En utilisant une calculatrice, proposer une résolution graphique de l'équation f(x) = g(x)
Valider par le caclul les solutions proposées.
3/Proposer alors des solutions éventuelles au problème de al-khuwarizmi.
4/Pour résoudre son problème al-khuwarizmi a eu l'idée de découper BEFC en deux rectangles de mêmes dimensions ( x et 2 ) et de former le grand carré ci-contre : 
Recopier et compléter l'égalité : x² + 4x = (x+2)² -....
En déduire la résolution algébrique de l'équation et les solutions du problème de al-Khuwarizmi.
5/En utilisant l'égalité de la question 4/, résoudre algébriquement sur IR les équations :
a) x² = -4x + 3 b) x² + 4x = -1 c) x² + 4x = -5
MErci d'avance pour votre aide
Merci merci et encore mille fois merci 
Pourrais tu m'aider pour la dernière partie de mon DM?
ici le lien : https://www.ilemaths.net/sujet-difficulte-sur-un-dm-partie-2-323428.html
*** message déplacé ***
Bonjour
Ce sujet a déjà été traité de très nombreuses fois, ici. Pour trouver les topics concernés, il faut utiliser la fonction Recherche représentée par une loupe dans le cadre en haut , avec le mot
al-Khwarizmi
Bonne recherche !
je ne trouve pas de lien relatant du même problème que le miens!
Aurait-tu un lien ou alors pourrait-tu m'expliquer?
bonsoir,
1/a) Ecrire l'aire du rectangle AEFD en fonction de x.
a(aefd)=x*x +4*x=x²+4x
b) En déduire l'équation que doit vérifier x pour répondre au problême.
x²+4x=21
2/Soit les fonctions f et g définies par IR par :
f(x) = x² g(x) = -4x + 21
En utilisant une calculatrice, proposer une résolution graphique de l'équation f(x) = g(x)
abscisse des points de concours de la droite et de la parabole x=3 ou x=-7
Valider par le caclul les solutions proposées.
quand x=3-->(3)²+4*3-21=0
quand x=-7--->(-7)²+4(-7)-21=49--28-21=0
3/Proposer alors des solutions éventuelles au problème de al-khuwarizmi.
une longueur doit être positive don x=-7 n'est pas une solution au problème
Recopier et compléter l'égalité : x² + 4x = (x+2)² -....
x²-4x est le début d'une identité remarquable x*x+2*2*x+2²
donc x² + 4x = (x+2)² -4
En déduire la résolution algébrique de l'équation et les solutions du problème de al-Khuwarizmi.
(x+2)²-4=21
(x+2)²-25=0
on a un a²-b²=(a-b)(a+b) avec a²=(x+2)²--->a=x+2 et b²=25--->b=5
donc (x+2-5)(x+2+5)=0
(x-3)(x+7)0
si ab=0, alors a=0 ou b=0
donc x=3 et x=-7
on elimine x=-7 (voir plus haut)
5/En utilisant l'égalité de la question 4/, résoudre algébriquement sur IR les équations :
a) x² = -4x + 3 b) x² + 4x = -1 c) x² + 4x = -5
a) x² = -4x + 3
x²+4x-3=0
(x+2)²-4-3=0
(x+2)²-7=0
(x+2-V7)(x+2+V7)=0
donc x=-2+V7 ou x=-2+V7
b) x² + 4x = -1
x²+4x+1=0
(x+2)²-4+1=0
....
c) x² + 4x = -5
(x+2)²-4=-5
(x+2)²=-5+4
(x+2)²=-1
un carré ne peut être .....
Merci gwendolin,
aujourd'hui j'essaye de répondre grâce à ton aide et je poste ma rédaction au propre.
Encore merci et bonne journée!
Voilà j'ai rédigé en fonction de l'aide que tu m'as donné!
Peut-tu me dire si la rédaction est bonne?
(Pour les dessins et l'énoncé se référer au premier post)
1/a) Ecrire l'aire du rectangle AEFD en fonction de x.
>J'écris l'aire du rectangle AEFD en fonction de x :
A (AEFD) = AD * AE
A (AEFD) = x * (x + 4)
A (AEFD) = x² + 4x
b) En déduire l'équation que doit vérifier x pour répondre au problème.
>Je déduis l'équation que doit vérifier x pour répondre au problème :
A (AEFD) = 21
x² + 4x = 21
2/Soit les fonctions f et g définies par IR par :
f(x) = x² g(x) = -4x + 21
En utilisant une calculatrice, proposer une résolution graphique de l'équation f(x) = g(x)
Valider par le caclul les solutions proposées.
>Grâce à la calculatrice je peux proposer une résolution graphique de l'équation f(x) = g(x) pour x = 3 et pour x = -7, car ceux sont deux abscisses des points de concours des deux fonctions f(x)=x² et g (x) = -4x + 21.
>Je peux alors vérifier par le calcul les solutions proposées grâce à l'équation que doit vérifier x pour répondre au problème :
.pour x = 3
x² + 4x = 21
éq à (3)² + 4*(3) = 21
éq à 9 + 12 = 21
éq à 21 = 21
L'équation pour x = 3 est alors vérifiée.
.Pour x = -7
x² + 4x = 21
éq à (-7)² + 4*(-7) = 21
éq à 49 + (-28) = 21
éq à 21 = 21
L'équation pour x = -7 est alors vérifiée.
3/Proposer alors des solutions éventuelles au problème de al-khuwarizmi.
>Comme une longueur doit être positive alors x=-7 n'est pas une solution au problème. Donc je propose x = 3 pour résoudre le problème du mathématicien arabe al-Khuwarizmi.
4/Pour résoudre son problème al-khuwarizmi a eu l'idée de découper BEFC en deux rectangles de mêmes dimensions ( x et 2 ) et de former le grand carré ci-contre :
Recopier et compléter l'égalité : x² + 4x = (x+2)² -....
En déduire la résolution algébrique de l'équation et les solutions du problème de al-Khuwarizmi.
>Je complète l'égalité : x² + 4x = (x+2)² -.... en complètent les pointillés par l'aire du grand carré. Donc :
x² + 4 x = ( x + 2) ² - 4
>Je peux en déduire la résolution algébrique de l'équation :
x² + 4 x = ( x + 2) ² - 4
éq à x² + 4 x = (x+2)²-(2)²
éq à x² + 4x = (x+2-2)(x+2+2)
éq à x(x+4) = x(x+4)
L'équation est bien vérifiée.
>Je peux déduire las solutions du problème de al-Khuwarizmi :
(x+2)² -4 = 21
éq à (x+2) ² - 25 = 0
éq à (x+2)² -5² = 0
éq à (x+2-5)(x+2+5) = 0
éq à (x-3) (x+7) = 0
éq à x - 3 = 0 ou x + 7 = 0
éq à x = 3 ou x = -7
S={3;-7}
J'élimine -7 comme prouvée dans le 3)
5/En utilisant l'égalité de la question 4/, résoudre algébriquement sur IR les équations :
a) x² = -4x + 3 b) x² + 4x = -1 c) x² + 4x = -5
a) x² = -4x + 3
x²+4x-3=0
(x+2)²-4-3=0
(x+2)²-7=0
(x+2-V7)(x+2+V7)=0
donc x=-2+V7 ou x=-2+V7
b) x² + 4x = -1
x²+4x+1=0
(x+2)²-4+1=0
(x+2)² - V3² = 0
(x+2-V3)(x+2+V3) = 0
donc x+2-V3 = 0 ou X+2+V3 = O
x = -2 + V3 ou x = -2 -V3
c) x² + 4x = -5
(x+2)²-4=-5
(x+2)²=-5+4
(x+2)²=-1
un carré ne peut être négatif donc il n'y a pas de solution possible.
Est-ce bon? Merci de vos réponses!
J'ai besoin de vérification de ma rédaction de votre part! Merci 
https://www.ilemaths.net/img/forum_img/0323/forum_323428_1.jpg
Voilà j'ai rédigé en fonction de l'aide que tu m'as donné!
Peut-tu me dire si la rédaction est bonne?
(Pour les dessins et l'énoncé se référer au premier post)
1/a) Ecrire l'aire du rectangle AEFD en fonction de x.
>J'écris l'aire du rectangle AEFD en fonction de x :
A (AEFD) = AD * AE
A (AEFD) = x * (x + 4)
A (AEFD) = x² + 4x
b) En déduire l'équation que doit vérifier x pour répondre au problème.
>Je déduis l'équation que doit vérifier x pour répondre au problème :
A (AEFD) = 21
x² + 4x = 21
2/Soit les fonctions f et g définies par IR par :
f(x) = x² g(x) = -4x + 21
En utilisant une calculatrice, proposer une résolution graphique de l'équation f(x) = g(x)
Valider par le caclul les solutions proposées.
>Grâce à la calculatrice je peux proposer une résolution graphique de l'équation f(x) = g(x) pour x = 3 et pour x = -7, car ceux sont deux abscisses des points de concours des deux fonctions f(x)=x² et g (x) = -4x + 21.
>Je peux alors vérifier par le calcul les solutions proposées grâce à l'équation que doit vérifier x pour répondre au problème :
.pour x = 3
x² + 4x = 21
éq à (3)² + 4*(3) = 21
éq à 9 + 12 = 21
éq à 21 = 21
L'équation pour x = 3 est alors vérifiée.
.Pour x = -7
x² + 4x = 21
éq à (-7)² + 4*(-7) = 21
éq à 49 + (-28) = 21
éq à 21 = 21
L'équation pour x = -7 est alors vérifiée.
3/Proposer alors des solutions éventuelles au problème de al-khuwarizmi.
>Comme une longueur doit être positive alors x=-7 n'est pas une solution au problème. Donc je propose x = 3 pour résoudre le problème du mathématicien arabe al-Khuwarizmi.
4/Pour résoudre son problème al-khuwarizmi a eu l'idée de découper BEFC en deux rectangles de mêmes dimensions ( x et 2 ) et de former le grand carré ci-contre :
Recopier et compléter l'égalité : x² + 4x = (x+2)² -....
En déduire la résolution algébrique de l'équation et les solutions du problème de al-Khuwarizmi.
>Je complète l'égalité : x² + 4x = (x+2)² -.... en complètent les pointillés par l'aire du grand carré. Donc :
x² + 4 x = ( x + 2) ² - 4
>Je peux en déduire la résolution algébrique de l'équation :
x² + 4 x = ( x + 2) ² - 4
éq à x² + 4 x = (x+2)²-(2)²
éq à x² + 4x = (x+2-2)(x+2+2)
éq à x(x+4) = x(x+4)
L'équation est bien vérifiée.
>Je peux déduire las solutions du problème de al-Khuwarizmi :
(x+2)² -4 = 21
éq à (x+2) ² - 25 = 0
éq à (x+2)² -5² = 0
éq à (x+2-5)(x+2+5) = 0
éq à (x-3) (x+7) = 0
éq à x - 3 = 0 ou x + 7 = 0
éq à x = 3 ou x = -7
S={3;-7}
J'élimine -7 comme prouvée dans le 3)
5/En utilisant l'égalité de la question 4/, résoudre algébriquement sur IR les équations :
a) x² = -4x + 3 b) x² + 4x = -1 c) x² + 4x = -5
a) x² = -4x + 3
x²+4x-3=0
(x+2)²-4-3=0
(x+2)²-7=0
(x+2-V7)(x+2+V7)=0
donc x=-2+V7 ou x=-2+V7
b) x² + 4x = -1
x²+4x+1=0
(x+2)²-4+1=0
(x+2)² - V3² = 0
(x+2-V3)(x+2+V3) = 0
donc x+2-V3 = 0 ou X+2+V3 = O
x = -2 + V3 ou x = -2 -V3
c) x² + 4x = -5
(x+2)²-4=-5
(x+2)²=-5+4
(x+2)²=-1
un carré ne peut être négatif donc il n'y a pas de solution possible.
https://www.ilemaths.net/img/forum_img/0323/forum_323428_2.jpg
Est-ce bon? Merci de vos réponses!
*** message déplacé ***

 upup
upup
