Désolé pour la feuille scannée en entier, donc j'écris ici l'énoncé de cet exercice :
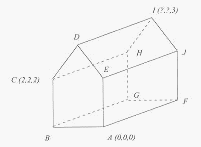
Calculez la distance entre l'un des deux plans du toit à double pente et la droite définie par l'intersection du plan du sol et du plan vertical coupant, dans le sens de la longueur, la maison en deux parties égales. La réponse étant Racine de 6.

Merci d'avance

Bonjour,

C'est difficile de répondre comme ça. Est-ce qu'il y a toutes les informations ? (par exemple a-t-on des égalités de longueur) De plus quels outils mathématiques peut-on utiliser ? Calcul vectoriel, analytique ...

Bonsoir,
Oui il y a une remarque que j'ai oublié de mentionner :

Il s'agira de considérer que : le plan du sol est le plan Oxy; le plan CEJH est parallèle au plan du sol; les plans ABCDE, AEJF, FGHI, BCHG sont perpendiculaires entre eux et verticaux ; les projections orthogonales de D et I sur le plan du sol tombent respectivement au milieu de AB et FG; la droite DI est parallèle au plan du sol.

La méthode je l'ai : établir l'équation du plan du pignon, puis grâce au vecteur normal à ce plan, l'équation de la droite AF, puis du point F, etc.

mais je n'arive pas à l'appliquer....


Merci pour cette réponse rapide. ça me fait plaisir !

bonsoir,

Voilà comment j'essaierais :

Faites une coupe de la maison et travaillez dans le plan ABD.
Prolongez (DE) pour venir couper (AB) en K. Soit L le milieu de  [AB]
Ce que vous recherchez, c'est la hauteur LH dans le triangle DLK...
que l'on doit bien pouvoir déterminer simplement en passant
par égalité d'aire (base*hauteur/2) dans le triangle DLK.

...

Merci pgeod pour ta réponse mais (je ne sais pas si tu as vu le message que j'ai posté à la même heure que toi) je dois utiliser la méthode du prof'... sauf que je n'arrive pas à l'appliquer...

help... ! J-6 ... =(

Bonsoir
peux-tu recopier les coordonnées des points ? (j'ai la vue qui baisse, je n'arrive pas à les lire sur la photo ...)

oui biensûr donc A(0,0,0) , C (2,2,2) , I ( ?, ?, 3)

voilà merci d'avance =)