Inscription / Connexion Nouveau Sujet
Distance d'un point à une courbe
Bonsoir, j'ai un dm pour demain dans lequel on nous donne :
La courbe Cf est la courbe représentative de :
f(x) = e^-2x +3
B (-4;2)
On admet que la distance BM admet un minimum quand M décrit la courbe Cf.
Ce minimum est appelé distance du point B à la courbe Cf.
On veut déterminer la distance de B à la courbe Cf.
1- a. A l'aide de Geogebra, réaliser une figure dynamique correspondant à la situation
-> ça c'est bon y'a pas de soucis
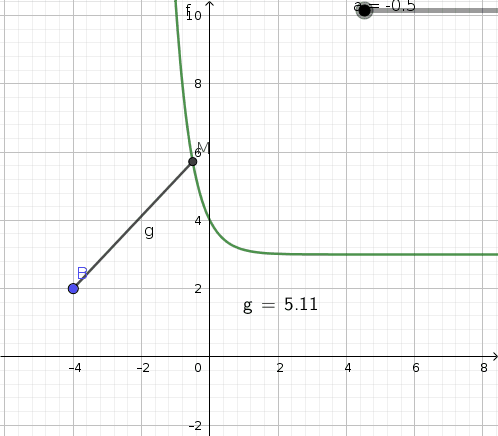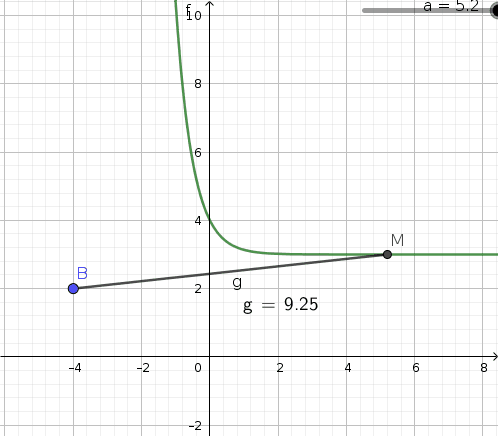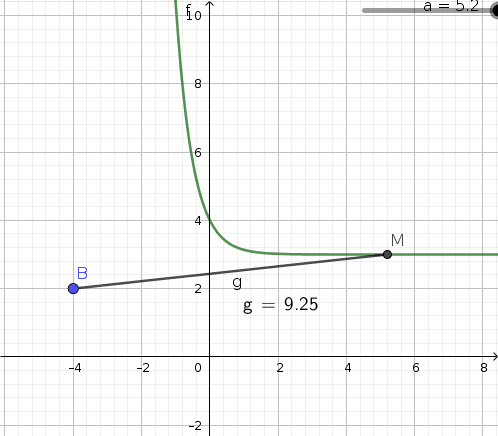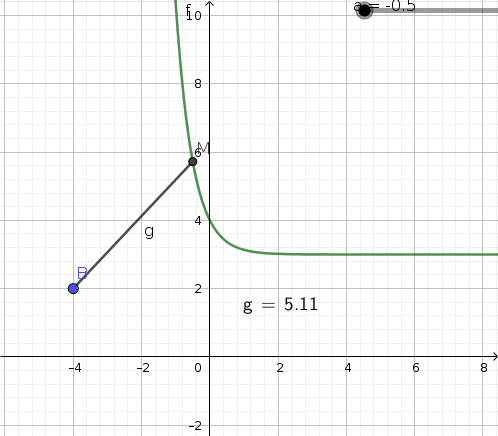
b. Faire une conjecture sur la position du point M pour laquelle la distance BM semble minimale. On appelle Mo ce point.
-> j'ai trouvé qu'en plaçant le point M en (0;4) la distance semblait être minimale, c'est donc ma conjecture.
2. On se propose de déterminer la valeur exacte de la distance du point B à la courbe Cf.
A. Proposer une méthode pour déterminer Mo et la distance du point B à la courbe Cf.
B. Mettre en œuvre
C. Comparer avec la conjecture émise
Voilà voilà... À partir de la 2.a je sais pas trop comment partir... Si vous pouvez m'aider merci d'avance
Bonsoir !
Tu prends un point sur la courbe, tu calcules la distance
en fonction de
et tu cherches le minimum de cette fonction.
Merci pour cette réponse ! D'ailleurs si un modérateur passe par là, désolé j'ai posté deux fois sans faire exprès, un message d'erreur me disait que mon topic n'avait pas pu être posté
Salut,
Tu dois certainement te souvenir de la formule donnant la distance entre deux points dans un repère, non ?
Salut ! Alors oui je m'en rappelle c'est √(xb-xa) ^2 - (yb-ya) ^2
Et donc de là j'ai comme inconnues les coordonnées de M ?
bonsoir
cela dit, pas la peine de s'encombre avec la racine carrée ...
BM sera minimal ssi BM² l'est.
appelle f(x)=BM²
tu calcules f'(x)
bof...
tu calcules f"(x)
signe très facile à étudier
tu "remontes"
tu en déduis le signe de f'(x)
et les variations de f
fini
salut, un petit air de deja vu ![]() Signe de dérivée
Signe de dérivée