Inscription / Connexion Nouveau Sujet
Distance maximale dans l'espace.
Bonjour ,
Merci d'avance. 
On considère un cube ABCDEFGH d'arête 1.
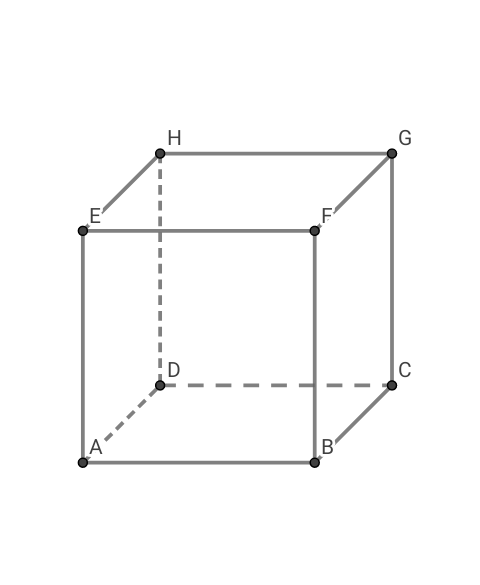
Dans tout l'exercice , l'espace est rapporté au repère .
On note K le barycentre des points pondérés (D , 1) et (F , 2).
Partie A
1) Montrer que le point K a pour coordonnées (2/3 ; 2/3 ; 2/3).
2) Montrer que les droites (EK) et (DF) sont orthogonales.
3) Calculer la distance EK.
Partie B
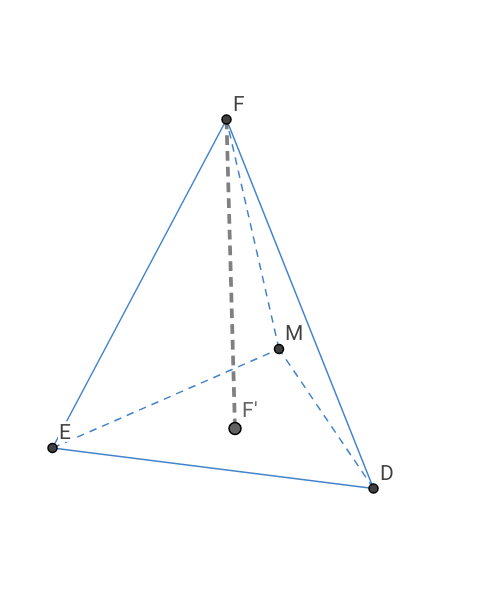
Soit M un point du segment [HG].
On note m=HM (m est donc un réel appartenant à [0 ; 1] ).
1) Démontrer que , pour tout réel m appartenant à l'intervalle [0 ; 1] , le volume du tétraèdre EMFD , en unité de volume , est égal à 1/6.
2) Démontrer qu'une équation cartésienne du plan (MFD) est (-1+m)x+ y -mz=0.
3) On note dm la distance du point E au plan (MFD).
a) Démontrer que , pour tout réel m appartenant à l'intervalle [0 ; 1] , .
b) Déterminer la position de M sur le segment [HG] pour laquelle la distance dm est maximale.
c) En déduire que lorsque la distance dm est maximale , le point K est le projeté orthogonal de E sur le plan (MFD).
Réponses
Partie A
1) On a : K= bar{(D , 1) ;(F , 2)} avec D(0 , 0 , 0) et F(1 , 1 , 1).
Donc
D'où K(2/3 ; 2/3 ; 2/3).
2) On a E(1 , 0 , 1) ; K(2/3 , 2/3 , 2/3) ; D(0 , 0 , 0) et F(1 , 1 , 1).
et
sont des vecteurs directeurs des droites (EK) et (DF).
et
Donc

, d'où (EK) et (DF) sont orthogonales car n'ont aucun point en commun (E ≠ K ≠ D ≠ F).
3)
Partie B
1) Le volume d'un tétraèdre est égal au tiers du produit de l'air de sa base par sa hauteur.
Comment déterminer l'air d'une base et sa hauteur d'un tel tétraèdre ?
Bonsoir,
B1) Pour calculer le volume du tétraèdre EMFD, je choisirais pour celui-ci le point D comme sommet et le triangle EMF comme base.
Ok mais le problème est comment déterminer l'air du triangle EMF sachant que M est un point quelconque de [HG] ?
Les distances EM , FM.. du tétraèdre EMFD ne sont pas constantes. Elles dépendent de la position de M sur le segment [HG].
Bonjour,
ta hauteur issue de F est quasiment impossible à calculer à ce stade
et tout autant l'aire de ta base MED
la bonne méthode est celle donnée par Priam
la base MEF et la hauteur issue de D,
perpendiculaire issue de D au plan (HEF), qui est un segment fixe indépendant de la position de M
une hauteur ne "tombe" pas forcément à l'intérieur de la base
c'est comme pour un triangle quand il a un angle obtus
Je comprends , H=DH=1
Maintenant l'air A de la base MEF :
A=(1/2)b'×h
Or la hauteur h du triangle MEF dépend de la position du point M. Aussi l'aire b' de la base MEF..
la hauteur h du triangle MEF
la ?? tout triangle à 3 hauteurs !
de laquelle parles tu ?
Fait une figure de la face HGFE [ à plat, en vraie grandeur ], place le point M ....quelle hauteur traces-tu ?
et puis ce qui compte ce n'est pas la hauteur (le segment) en elle même, c'est sa mesure !
oui, (EH n'est pas la hauteur mais est égale à la hauteur issue de M)
et donc ?
Aire de MEF ?
Volume de DEFM ?
puis la suite ?
Partie B
1) Le volume du tétraèdre EMFD VEMFD=1/3× B × H
B : l'aire du triangle EMF
H : la hauteur du tétraèdre EMFD issue du point De.
* On a H= DH= 1
* ; h la hauteur du triangle EMF issue du point M : h=EH= 1 ;
b la mesure du côté EF : b=EF=1.
==> B= 1/2
Donc VEMFD= 1/3×1/2×1=1/6
V EMFD = 1/6.
2) Je ne vois pas vraiment comment faire..
OK pout le calcul du volume
question 2)
l'espace est rapporté au repère
...
2) Démontrer qu'une équation cartésienne du plan (MFD) est (-1+m)x+ y -mz=0.
et donc déja quelles sont les coordonnée de M (en fonction de m, en littéral) et des autres points dans ce repère ?
ensuite :
on peut comprendre la question de deux façons : une difficile, une facile
- à partir des coordonnées uniquement, on élabore une équation du plan
(et on devrait obtenir une équation équivalente à celle qui est donnéé)
- vérifier que avec l'équation donnée, ce plan d'équation donnée est bien le plan (MFD) c'est à dire passe par M, par F et par D
que penses tu qu'il est le plus facile de faire ?
de toute façon les deux démarches "démontrent que", aussi bien l'une que l'autre sans aucun problème de logique.
M(0 ; HM=m ; 1) soit M(0 ; m ; 1)
F(1 ; 1 ;1)
D(0 ; 0 ;0)
*(-1+m)×0 +m -m×1 = m-m=0
donc le plan d'équation (-1+m)x + y -mz = 0 passe par le point M.
* (-1+m)×0 +0-m×0=0
donc le plan d'équation (-1+m)x + y -mz = 0 passe par le point D.
* (-1+m)×1 +1 -m×1 =-1+m+1-m=0
donc le plan d'équation (-1+m)x + y -mz = 0 passe par le point F.
==> (-1+m)x +y -mz = 0 est une équation du plan (MFD).
oui.
ensuite :
que dit le cours (formule ?) sur la distance d'un point à un plan ?
vecteur normal à un plan ?
mais KE a déja été calculé partie A 3. !!
la question partie B 2c ne nécessite aucun calcul
seulement la comparaison de ces deux valeurs pour conclure.
nota :
on n'utilise nulle part le volume calculé question B 1.
dommage...
en effet ce volume constant montre que la distance maximale de E au plan (MFD) (c'est la hauteur du tétraèdre issue de E) est lorsque l'aire du triangle MFD est minimale
c'est à dire, puisque dans ce triangle sa base DF est fixe, lorsque la distance de M à (DF) est minimale.
ce qui correspond à la distance entre les droites (HG) et (DF) : perpendiculaire commune à ces deux droites
on montre que si P est le milieu de [GH] et O le centre du cube (milieu de [DF]) cette perpendiculaire commune est (OP) (que (OP) est  (GH) et à (DE))
(GH) et à (DE))
et donc la distance minimale de M à (DF) est OP, quand M est en P
on retrouve sans calcul que le maximum cherché est quand m = 1/2
J'ai pas compris votre dernier message..
Comment pourrait on faire intervenir le volume du tétraèdre EMFD dans un calcul ici ?
le volume est égal à 1/3 de l'aire de n'importe laquelle des bases * la hauteur correspondante
je choisis la base MFD et la hauteur issue de E
cette hauteur issue de E est justement la distance de E au plan (MFD) que l'on cherche à maximiser.
appelons la [EN]
donc 1/3 EN * aire(MFD) = 1/6, le volume indépendant de M et constant déja calculé
donc EN est maximum quand l'aire(MFD) est minimum, puisque le produit est constant.
etc (relire le message précédent)
il n'y a aucun calcul du tout, que du raisonnement.
et
on montre que si P est le milieu de [GH] et O le centre du cube (milieu de [DF]) cette perpendiculaire commune est (OP) (que (OP) est ⊥ (GH) et à ⊥ (DF))
O centre du cube appartient au plan médiateur de [HG]
terminé
montrons que (OP) ⊥ (DF) :
les triangles PGF et PHD rectangles en G et en H avec PG = PH et GF =HD sont égaux (isométriques) donc PF = PD
le triangle PFD isocèle en P voit donc sa médiane [PO] perpendiculaire à sa base [DF}
là non plus aucun calcul, même si on peut faire ça "bourrin" en calculant des produits scalaires ...