Bonjiur

les moteurs de recherche et les copier-coller ne peuvent pas extraire du texte d'une image
il est donc obligatoire de recopier au moins le début de l'énoncé
comme exigé dans A LIRE AVANT DE POSTER OU DE RÉPONDRE, MERCI
et comme tu as forcément dû le lire en joignant ton image

extrait de la FAQ du forum :

Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?

Vous souhaitez ajouter une image ou un pdf à votre message . Veuillez obligatoirement respecter ces règles :

Énoncé d'exercice ou de problème :

Pour les énoncés courts (moins de 5 lignes sur une feuille A4) :
La recopie est obligatoire.
L'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !

Pour les énoncés longs  :
Les 5 premières lignes sont à recopier pour aider l'archivage des sujets sur le site.
Cela fait, l'énoncé dans sa totalité, pourra alors être joint en image (choisir Img) ou en pdf (choisir Pdf ) mais dans le respect des droits d'auteurs en vigueur. Pour les pdf, merci d'en préciser la source.

Recherches (même non abouties) de l'exercice :
Elles doivent être obligatoirement recopiées, et ce, dès la demande d'aide.
l'option d'attachement d'image n'est donc à utiliser que pour représenter une figure, un tableau ou un graphique, pas du texte !
Les formats autorisés sont exclusivement les suivants : gif, jpg, jpeg, et png. La taille d'un fichier est limitée à 2 MO maximum pour une image et à 500 ko pour un pdf.

Le non respect de ces règles entraînera la suppression du contenu de votre sujet (même si des réponses ont été apportées) et éventuellement la suspension de votre compte !

Seule exception : Dans le forum détente, des réponses longues et élaborées , contenant plusieurs images explicatives, pourront être postées sous forme d'image ou de pdf. Les énoncés, quant à eux, devront toujours être rédigés sur le site (indispensable pour le référencement).

D'accord merci beaucoup, j'ai du lire en diagonale merci.
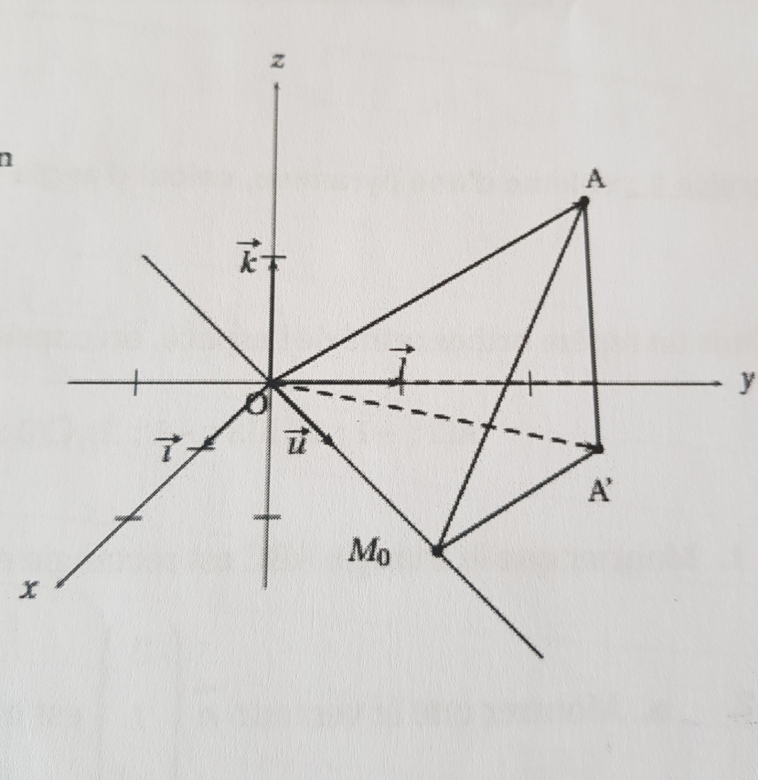
Dans un repère orthonormé (0; i,j,k) on considère:

• le point A de coordonnées (I; 3; 2),
• le vecteur u de coordonnées (1;1;0)
• la droite d passant par l'origine O du repère et admettant pour vecteur directeur u.

Le but de cet exercice est de déterminer le point de d le plus proche du point A et d'étudier quelques propriétés de ce point.
On pourra s'appuyer sur la figure ci-contre pour raisonner au fur et à mesure des questions.
1. Déterminer une représentation paramétrique de la droite d.
j'ai trouvé: x=t, y=t, z=0

2.Soit t un nombre réel quelconque, et M un point de la droite d, le point M ayant pour coordonnées (t;t; 0).
a On note AM la distance entre les points A et M. Démontrer que : AM^2 = 2t^2-8t + 14
cette question j'ai réussi

b. Démontrer que le point M⁰ de coordonnées
(2; 2; 0) est le point de la droite d pour lequel la distance AM est minimale. On admettra que la distance AM est minimale lorsque son carré AM est minimal.
C'est là où je bloque car je me suis dit qu'il fallait peut-être remplacer les t de AM^2 par M⁰ mais je n'arrive pas à continuer

3. Démontrer que les droites (AM⁰) et d sont orthogonales.
cette question aussi je l'ai faite en faisant le produit scalaire qui doit être égal à 0

4. On appelle A' le projeté orthogonal du point A sur le plan d'équation cartésienne z = 0. Le point A' admet donc pour coordonnées (1; 3; 0). Démontrer que le point M⁰ est le point du plan (AA' M⁰) le plus proche du point O, origine repère.
cette question aussi je suis bloqué

5.Calculer le volume de la pyramide OM,A' A. On rappelle que le volume d'une pyramide est donné par: V =Bh, où B est l'aire d'une base et h est la hauteur de la pyramide correspondant à cette base.

Voilà voilà, je vous joins la figure qui y est associée :

Bonjour,
2. Cherche le minimum de AM². le segment AM sera aussi de longueur minimale pour la valeur de  t  obtenue.
4. Démontre que la droite OM_o est perpendiculaire à deux droites du plan (AA'M_o).

Je n'ai pas très bien compris comment chercher le minimum de AM²

2b)
AM^2 = 2t^2-8t + 14
AM² minimale = minimum d'une fonction du second degré = cours
donne la valeur de t et les coordonnées du point cherché.
on vérifie alors que c'est M₀

4) prouver de façon géométrique ou avec des produits scalaires que OM_o est orthogonale au plan (AA' M_o) :
car alors pour tout autre M du plan, dans le triangle OMM₀ l'hypoténuse OM > OM₀)

comme disait Priam (que je salue) entre temps d'ailleurs.

On a établi au 2 l'expression de AM² en fonction de  t . C'est un trinôme du second degré.
Il s'agit donc de déterminer la valeur de  t  qui lui donne sa valeur minimale.

D'accord merci beaucoup
Du coup comme c'est une fonction du second degré j'ai fait t=-b/2a et j'ai trouvé t=2 puis j'ai remplacé dans AM² et j'ai trouvé que la distance minimale est de 6.

Pour le 4 j'ai aussi compris et j'ai trouvé avec le produit Scalaire.

Du coup grâce à la représentation parametrique de (d), je remplace t par 2 et je trouve bien que le point est (2;2;0) soit le point M.
Est-ce bien cela ?

on ne demande pas de calculer dans la 2b la valeur de la distance minimale, mais de prouver que c'est en M₀

une fois que tu as t =2 tu reportes dans l'équation de la droite pour vérifier si oui ou non c'est bien le point M₀

2. D'accord. On demande au paragraphe  b  d'en déduire les coordonnées du point M correspondant.
4. Très bien (pour une certaine droite du plan AA'M_o, point n'est besoin  de produit scalaire).

D'accord merci beaucoup !!
Et pour la question 5, la hauteur est bien AM ?

dans une telle pyramide (tétraèdre) n'importe laquelle; des 4 faces peut être choisie comme base
et la hauteur est la perpendiculaire à cette base (le plan) issue du sommet opposé.

AM est perpendiculaire à quel plan ??
surtout qu'on te parle de M_o pas de M quelconque.

cherche parml les perpendiculaires à des plans dans la figure.
(2 choix possibles)

Donc si je prend le plan AA'M⁰ la droite AA' est perpendiculaire à ce plan du coup ?

Ou plutôt AA' est perpendiculaire au plan AA'O

non
AA' est bien perpendiculaire au plan AA'M_o

une droite (UV) ne peut certainement pas être perpendiculaire au plan (UVW) puisque incluse dans ce plan !!

D'accord d'accord.
En tout je vous remercie beaucoup, vous m'avez beaucoup aidé.
Je vous souhaite une bonne fin de journée !
Encore merci !

de rien

il reste à finaliser le calcul numérique de ce volume.
(en utilisant certains résultats déjà obtenus et en les complétant)