Bonsoir,

à mon avis tu vas tourner en rond sur les définitions des opérations addition et multiplication.

pourquoi (comment démontrer) 2 fois 6 = 12 ?
pourquoi l'aire d'un rectangle est elle largeur multiplié par longueur ?

si on admet ce genre de trucs, une justification possible (une preuve est à mon avis hors de propos à ce niveau)
est de considérer l'aire de deux rectangles accolés :


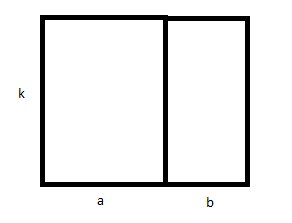
l'aire totale est la somme des aires des deux rectangles
donc k*(a+b) l'aire totale du rectangle de dimensions k et (a+b)
est égale à la somme des aires k*a et k*b.

Merci pour ta réponse Mathafou.
Je comprends, c'est une sorte d'Axiome.
Cependant, tu dis qu'une preuve est hors de propos à ce niveau ; en aurais-tu cependant une avec des notions du supérieur ?
Encore merci.

salut

avec une preuve de niveau supérieur ...

soit E un ensemble muni des opérations T et X

ces deux opérations possédant individuellement des propriétés .... (commutativité, associativité, ...) ou non ...

DEFINITION :: dire que X est distributive par rapport à T signifie simplement que pour tous a, b et c dans E la relation a X (b T c) = (a X b) T (a X c)

ce n'est pas un axiome c'est une définition

et celle-ci est vérifiée ou non pour deux opérations x et T d'un ensemble ....

ainsi / est distributive à droite par rapport à + mais pas à gauche ::

(a + b)/d = a/d + b/d mais d/(a + b) d/a + d/b

....

par contre * est distributive à droite et à gauche par rapport à +



un exercice d'application ::

Camille remplit des cagettes de fruits pouvant contenir k = 20 fruits

elle a remplit a = 10 cagettes hier et b = 15 cagettes aujourd'hui

calculer de deux façons différentes le nombres de fruits que Camille a rangé

mais bon c'est le même exemple que mathafou t'a fourni ...

DEFINITION :: dire que X est distributive par rapport à T signifie simplement que pour tous a, b et c dans E la relation a X (b T c) = (a X b) T (a X c) est vraie

Bonjour

ce n'est pas parce que c'est une définition qu'on ne peut pas prouver que * est distributive sur + dans N puis dans Z puis dans Q puis dans R ....
il me semble même qu'on nous le faisait faire du temps où on avait encore une construction axiomatique des ensembles de nombres, non ?

pour des entiers naturels : k*a signifie a+a+...+a, k termes a
k*b = b+b+b+...+b, k termes b

k*a + k*b = a+a+...+a+b+b+...+b = (a+b)+(a+b)+...+(a+b), par commutativité et associativité de l'addition (on peut changer les termes de place dans une somme comme bon nous semble, et coller des parenthèses là où on a envie)
et donc = k*(a+b)

etc etc

Je comprends tout à fait ton idée lafol.
Et dans ce cas, comment démontre-t-on le résultat dans Z, dans Q et dans IR ?
Merci pour votre aide.

c'est le genre de truc qu'on doit trouver dans les Bourbaki ....

en gros, l'idée pour construire Z à partir de N, c'est de définir une relation d'équivalence sur les couples (a,b) d'entiers naturels

(a,b) R (a',b') < == > a + b' = a' + b (vérifie que c'est bien une relation d'équivalence)

et un entier relatif est une classe d'équivalence pour cette relation d'équivalence. par la suite je noterai CL(a,b) la classe de (a,b)

on définit aussi une addition induite par + habituel de N : on constate que si (a,b) R(a',b'), et (c,d) R(c',d'), alors (a+c,b+b)R(a'+c',b'+d'), ce qui légitime de poser CL(a,b) + CL(c,d) = CL(a+c, b+d)
on vérifie alors que cette loi est associative, commutative, que CL(0,0) (qui contient tous les (a,a) avec a dans N) est élément neutre, et que CL(a,b) admet un symétrique qui est CL(b,a) : notre nouvel ensemble est un groupe, muni de cette addition.

On montre alors que l'application f de N vers ce nouvel ensemble, qui à n associe f(n) = Cl(n,0), est un morphisme injectif : ça permettra d'identifier un entier naturel n avec CL(n,0) (de noter de la même manière un entier naturel et un entier relatif positif, à terme)

et puisque l'opposé de CL(n,0) qu'on va noter n est CL(0,n) = -CL(n,0), il devient naturel de noter aussi -n pour CL(0,n), et pour terminer, puisque CL(n,0) + CL(0,m) = CL(n,m), on notera simplement n-m pour CL(n,m)
en gros, les entiers relatifs positifs, identifiés aux entiers naturels = CL(n,0), les entiers relatifs négatifs, opposés des entiers naturels = CL(0,n)
On pourrait parler ici de la relation d'ordre, aussi

tu suis toujours ?

on va passer au produit ! je te préviens, c'est plus compliqué !

comme on a vu qu'à terme, CL(a,b) deviendra a-b, et CL(c,d) deviendra c-d, on sait ce qui nous reste à faire pour définir une multiplication sur cet ensemble de classes : on aimerait bien que ça marche "comme d'habitude" et que donc (a-b)(c-d) )= ac + bd - (ad + bc)

avant de définir Cl(a,b)*CL(c,d) = CL(ac+bd, ad+bc), il faut quand même s'assurer que ça ne dépend pas du représentant choisi pour les différentes classes, en clair, que si (a,b) R (a',b') et (c,d) R (c',d'), on aura encore (ac+bd, ad+bc) R (a'c'+b'd', a'd'+b'c')

c'est parti : on suppose donc a + b' = a' + b, et c + d' = c' + d

on multiplie ces égalités par c,d,a' et b' : ac + b'c = a'c + bc, a'd + bd = ad + b'd, a'c + a'd' = a'c' + a'd, et b'c' + b'd = b'c + b'd'

on additionne tout membre à membre : ac + b'c + a'd + bd + a'c + a'd'+ b'c' + b'd = a'c + bc+ ad + b'd+ a'c' + a'd + b'c + b'd'

on simplifie : ac + bd + a'd'+ b'c' = bc + ad + a'c' + b'd' ! c'est gagné ! magique, non ?


donc on pose CL(a,b)*CL(c,d) = CL(ac+bd, ad + bc)

au passage, la règle des signes, elle est là : si m et n sont des entiers naturels, m(-n) = CL(m,0)*CL(0,n) = CL(m*0 + 0*n, mn + 0*0) = -mn : le produit d'un positif par un négatif est un négatif

tu voulais prouver la distributivité ? il "suffit" de vérifier que CL(a,b)*(CL(c,d) + CL(c',d')) = CL(a,b)*CL(c,d) + CL(a,b)*CL(c',d') ...

ça a été la leçon 09 au CAPES, d'après Google .... tu trouveras plein de documents là dessus

ha oui bin vu lafol .... et merci pour ces révisions ...

en particulier on retrouve les astuces de calcul mental du genre ::

pour soustraire 27 de 114 on soustrait 30 de 117

car (114, 27) et (117, 30) sont deux éléments d'une même classe