Bonjour

Aurais-tu quelques exemples d'expressions où tu souhaites qu'on t'aide ?

Je voudrais que vous m'expliquer comment procéder avec (x-a) car je viens de lire mes cahiers de mathématique plusieurs fois et donc pour moi le reste c'est ok .
Si vous avez quelques exercices avec (x-a) ça sera parfait sinon je me débrouillerai pour en dénicher

Non mais je ne comprends pas, aurais-tu des exercices ^^

C'est ça que je voulais dire ^^

Ah ok^^
6x² + 11x + 5=

= ?

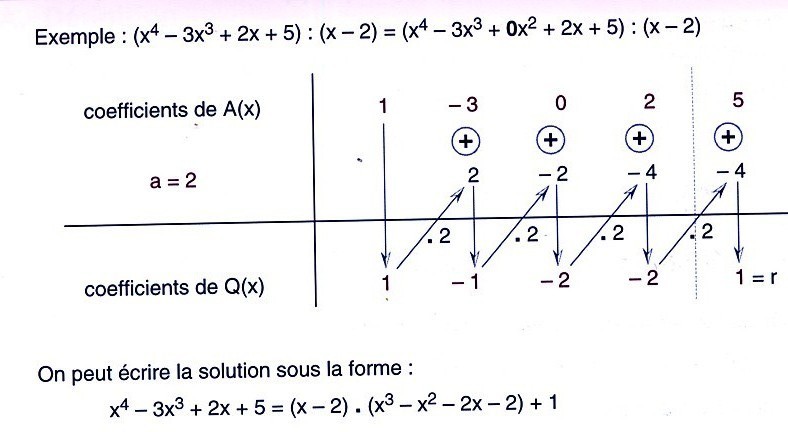
Je comprend avec P(x)

mais pas avec une division euclidienne

Enfin dans mon cour on divise 6x² + 11x + 5 par x + 1

Et un autre exercice avec une division euclidienne: x² - 5x + 6 par x - 2

PS:désolée du double poste

Avec P(x) pour le premier je fais

P(-1)= 6. (-1)² +11 . (-1) + 5 = 6 - 11 +5 = 0 Donc a = -1

Bonsoir aminosnip et Antoine !

aminosnip, tu es en fait en classe 3^ème en France, c'est l'équivalent du/de la 3^ème secondaire en Belgique (voir cette page : [lien]).

Pour revenir au sujet, les divisions de polynômes ne sont pas enseignées en France en 3^ème mais plutôt dans le supérieur, mais je n'en suis pas sûr.
Il y a un site intéressant qui en parle et qui pourra peut-être t'aider, le voici (clique sur la maison) : .

De rien.

Merci beaucoup !!
Sûr ce bonne soirée et à bientôt

Euh... de rien.

Alors, pour la division polynomiale, il s'agit d'une division très simple, c'est comme celle que tu fais d'habitude pour trouver un quotient:
Par exemple quand tu veux diviser 13 par 3:
Tu effectue la division ci-dessous:
Et c'est le même cas avec les polynômes. Voir la comparaison que je t'ai fait.. Si tu ne comprend pas, je peux encore t'expliquer, mais précise ta question pour éviter de perdre le temps.

Voici une methode

bonjour,

(6x²+11x+5)/(x+1)

quand x=-1, 6x²+11x+5=6-11+5=0
-->6x²+11+5=(x+1)(ax+b)
on développe
(x+1)(ax+b)=ax²+ax+bx+b=ax²+x(a+b)+b
on identifie les 2 expressions
a=6
a+b=11-->b=11-6=5

donc 6x²+11x+5=(x+1)(6x+5)