Inscription / Connexion Nouveau Sujet
Dm à faire
Bonjour, j'aimerais que vous m'aidiez parce que je suis bloqué.J'espere que vous aurez des réponses parce que je viens de m'inscrire merci.
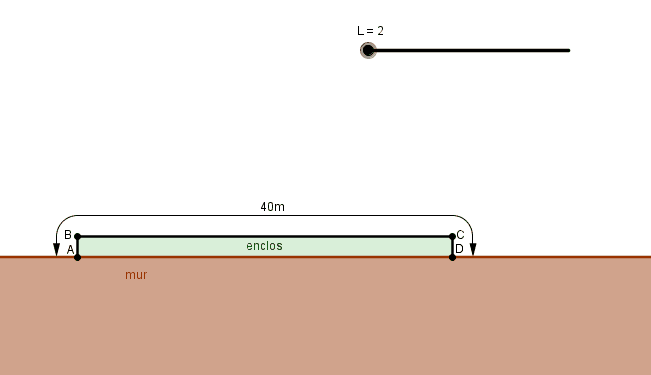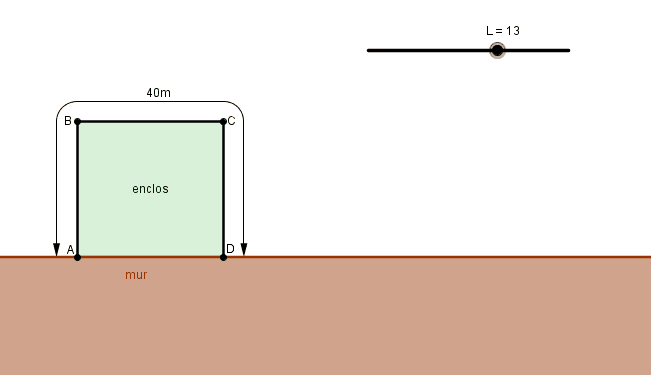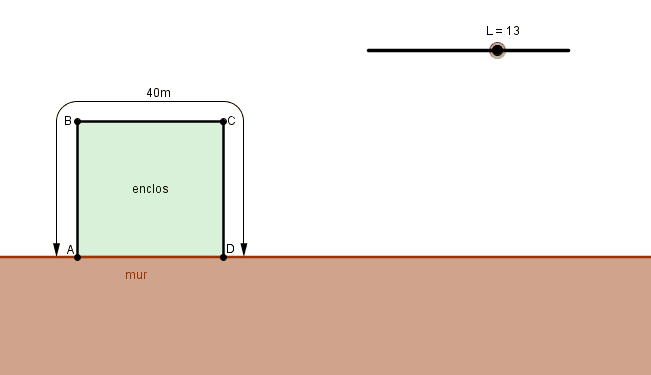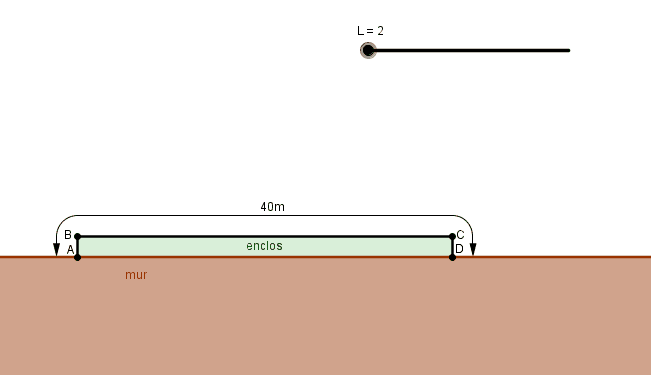
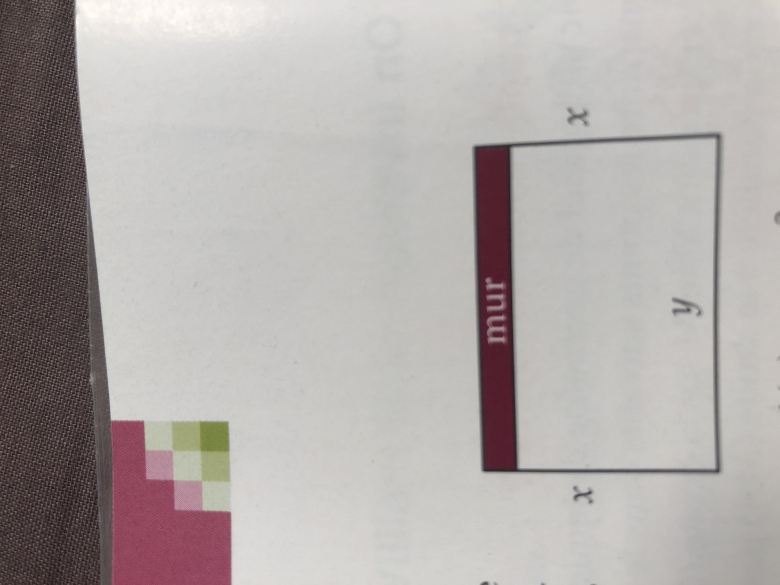
Contre le mur de sa grange, un fermier veut construire un enclos grillagé rectangulaire.Le 4ème côté est une partie du mur.Il dispose pour cela de quarante mètre de grillage pour clore trois côtés du rectangle et obtenir un enclos d'aire maximale.
1)Montrer que l'aire A(x) de l'enclos en fonction de x est égale à A(x)=-2x(au carre) +40x.
2)Tracer la courbe de la fonction A à la calculatrice sur l'intervalle [0;20].
3)En déduire le tableau de variation de la fonction À.
4)Montrer que A(x) est maximale lorsque sa longueur est égale au double de sa largeur.
5)A l'aide de la calculatrice, donner l'ensemble des nombres x pour lesquels A(x)<(ou égal) a 72.
Bonjour,
bof !!! un tel croquis ne représente pas du tout la réalité donc inutilisable
le mur va bien plus loin que les bords de l'enclos. (sinon il n'y a rien à faire varier !!)
animation :