Bonjour,

a) Parabole orientée vers les y positifs car le coeff de x² est positif.

b)=-(-1)/(2*1)=1/2

=f(1/2)=(1/2)²-1/2-3=1/4-2/4-12/4=-13/4

Donc S(1/2;-13/4) ou S(0.5;-3.25)

Donc f(x) décroît sur ]-inf;0.5] puis croît sur [0.5;+inf[

Tu fais un tableau avec des flèches bien sûr.

c) Tu as cette courbe ( Je vois pour l'algo ensuite ) :

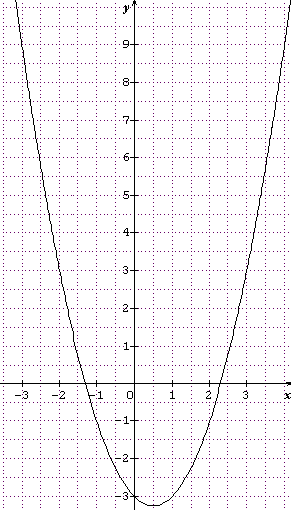
d)

merci beaucoup ! je viens de comprend pourquoi j'y arriver pas j'avais mis mes + a la place des - ^^'  

Voici les instructions pour l'algo sur Algobox. Tu remarqueras que la ligne "Fin si" n'est pas à sa place dans ce que l'on te donne.

Il faut définir la fct en bas de l'écran d'Algobox de la manière suivante :

F1(x)=pow(x,2)-x-3

J'ai rajouté la ligne 20.

L'algo donne :x₀ =2.3125

A taper :

1   VARIABLES
2     a EST_DU_TYPE NOMBRE
3     b EST_DU_TYPE NOMBRE
4     x EST_DU_TYPE NOMBRE
5   DEBUT_ALGORITHME
6     a PREND_LA_VALEUR 2
7     b PREND_LA_VALEUR 3
8     TANT_QUE (b-a>0.1) FAIRE
9       DEBUT_TANT_QUE
10      x PREND_LA_VALEUR (b+a)/2
11      SI (F1(x)>0) ALORS
12        DEBUT_SI
13        b PREND_LA_VALEUR x
14        FIN_SI
15        SINON
16          DEBUT_SINON
17          a PREND_LA_VALEUR x
18          FIN_SINON
19      FIN_TANT_QUE
20    AFFICHER "La valeur de x est : "
21    AFFICHER x
22  FIN_ALGORITHME
23
24 Fonction numérique utilisée :
25 F1(x)=pow(x,2)-x-3

notre professeur nous mettez toujours fin si en premier donc je ne sais pas mais merci encore maintenant je crois avoir compris grave a vous je peux finir seul a present merci

pouvais vous m'aider a faire mon algorithme ?

l'exercice:
2 Etude algorithmique :

a-Calculer f(2,5). Quel est son signe ?
En déduire un nouvel encadrement d'amplitude 0,5 de la solution cherchée.

b-On donne l'algorithme suivant :

Variables :
a,b,x sont des nombres
Traitement :
a prend la valeur 2
b prend la valeur 3
Tant que b-a>0,1 faire :
          x prend la valeur    (b+a)/2
         Si  f(x)>0
             alors b prend la valeur x
             sinon a prend la valeur x
         Fin si
Fin Tant que
Sortie
Afficher x

Appliquer cet algorithme pour compléter le tableau ci-dessous :


a b b- a test x f(x) Signe de f(x)
Etape 0 2 3 1 vrai
Etape 1
Etape 2
Etape 3
Etape 4


c-Quelle est la valeur affichée par l'algorithme ?
Que représente cette valeur concernant l'équation x²-x-3=0


3 Prolongement :

Dans l'algorithme, on modifie la ligne 6 avec « tant que b - a > 0,01 ».
A l'aide d'un logiciel, écrire ce nouvel algorithme et donner la valeur affichée.
Interpréter le résultat.

*** message déplacé ***

BONJOUR,

je pense que c'est par raport a l'exercice d'audessus xd je l'affiche :


En classe de seconde, on ne dispose pas de méthode pour résoudre l'équation :

                                            x²-x-3=0

On se propose ici de développer une méthode de recherche d'une « approximation » de la solution positive de cette équation.

Etude graphique :

Quelle est la nature de la représentation graphique de la fonction définie par f(x)=x²-x-3 ?

Vérifier que les coordonnées de son sommet sont S (0,5 ; - 3,25)
En déduire le tableau de variation de f sur l'intervalle [- 3 ; 3]

Tracer la courbe représentant la fonction f sur [- 3 ; 3] sur le repère ci-dessous.

En déduire un encadrement par deux entiers de la solution positive de l'équation x²-x-3=0

*** message déplacé ***

peu etre que les reponce vont t'aidé ^^

le orientée vers les y positifs car le coeff de x² est positif.

b) =-(-1)/(2*1)=1/2

=f(1/2)=(1/2)²-1/2-3=1/4-2/4-12/4=-13/4

Donc S(1/2;-13/4) ou S(0.5;-3.25)

Donc f(x) décroît sur ]-inf;0.5] puis croît sur [0.5;+inf[

Tu fais un tableau avec des flèches bien sûr.

c) Tu as cette courbe ( Je vois pour l'algo ensuite ) :

d)

Le graph montre que la solution positive x0 de f(x)=0 est telle que :

2 < x0 < 3

f(2.5)=2.5²-2.5-3=0.75 qui est positif.

Donc :

2 < x0 < 2.5

*** message déplacé ***

sinon je veux bien qu'on m'aide ou donne les reponces ma question XD

*** message déplacé ***

pouvais vous m'aider a faire mon algorithme ?

l'exercice:
2 Etude algorithmique :

b-On donne l'algorithme suivant :

Variables :
a,b,x sont des nombres
Traitement :
a prend la valeur 2
b prend la valeur 3
Tant que b-a>0,1 faire :
          x prend la valeur    (b+a)/2
         Si  f(x)>0
             alors b prend la valeur x
             sinon a prend la valeur x
         Fin si
Fin Tant que
Sortie
Afficher x

Appliquer cet algorithme pour compléter le tableau ci-dessous :


a b b- a test x f(x) Signe de f(x)
Etape 0 2 3 1 vrai
Etape 1
Etape 2
Etape 3
Etape 4


c-Quelle est la valeur affichée par l'algorithme ?
Que représente cette valeur concernant l'équation x²-x-3=0


3 Prolongement :

Dans l'algorithme, on modifie la ligne 6 avec « tant que b - a > 0,01 ».
A l'aide d'un logiciel, écrire ce nouvel algorithme et donner la valeur affichée.
Interpréter le résultat.

*** message déplacé ***

Bonjour,

Le multi-post est interdit, ici.

Lire ceci : ------>  "A lire avant de poster, ici. Merci" = Sujet ancien- ne plus donner ce lien-merci les gestionnaires de ce forum n'ont pas écrit ce topic, juste pour faire joli dans le décors !

et cela : ------> la FAQ = [lien]

*** message déplacé ***

je suis sincèrement désolé du multi-post mais j'aimerai u'on m'aide un tout petit peu pour que je comprenne comment faire ^^ c pas que je suis hyper nul mais presque ^^ et j'ai personne pour m'expliqué
merci et désolé du multi-post

*** message déplacé ***

le multi post n'est pas toléré ici, et le multi compte encore moins