Inscription / Connexion Nouveau Sujet
Dm algorithme.
On considère un parallélogramme ABCD.
1. Traduire cette information à l'aide d'une égalité vectorielle.
2. Exprimer les coordonnées du point D(XD; yD) en fonction des coordonnées des points A,B et C.
3. Créer un algorithme et un programme a la calculatrice qui a partir des coordonnées de quatre points A,B,C et D affiche si le quadrilatère ABCD est un parallélogramme ou non. Noter l'algorithme et le programme sur votre copie.
4. Tester votre programme et dire ce qu'affiche la calculatrice dans les deux cas suivants:
a. A(3;5); B(5;0); C(-1;-1) et D(-3;4)
b. A(3;2); B(5;1); C(-1;-2) et D(-3;0)
Merci a tous!
Ok, je me doute que, vu que tu es en seconde, tu n'as pas vu la relation: xy'-yx'=0 lorsque deux vecteurs sont colinéaires, je me trompe ?
D'accord ça m'arrange tant mieux !! 
Bon, prenons deux vecteurs de coordonnées (x;y) et
de coordonnées (x';y'). Avec ces vecteurs, on peut verifier leur colinéarité grâce à la relation xy'-yx'. S'ils sont colinéaires cette relation vaut 0 sinon elle n'est pas nulle. En résumé, si u et v sont colinéaires alors xy'-yx=0.
Pour ça, ça va ?
Ok, maintenant on peut créer un algoritme qui va AUTOMATISER la tâche suivante: dire qi 4 points forme un parallélogramme.
Est ce qu'il est demandé de le rédiger en langage courant/naturel ?
D'accord, mais c'est écrit "écrire un algorithme ET un programme"...
Je vais commencer par l'algorithme et il sera très simple de le programmer ensuite 
Bon, premièrement on doit déclarer les variables que l'on va utiliser par la suite. On en aura besoin de au total. 8 pour les coordonnées des points et 4 pour les coordonnées des vecteurs :
On prend, par exemple, pour coordonnées A(R;S), B(Z;T), C(M;N) et D(U;V), je prends directement des lettres capitales pour faciliter le transfert algorithme-programme... et pour les vecteurs AB(E;F) et DC(G;H) où E=Z-R, F=T-S, G=M-U et H=N-V.
ça va toujours ? sinon fais un dessin, ça facilitera les choses... 
Parfait !
On doit vérifier que le quadrilatère est un parallélogramme donc on doit aussi vérifier que les vecteurs AD et BC sont colinéaires donc on calcule leurs coordonnées AD(I;J) et BC(K;L) où I=M-Z, J=N-T, K=U-R et L=V-S
On rajoute donc 4 variables, ce qui fait 16...
Voici un exemple : AB et DC sont col. mais AD et BC n'y sont pas...
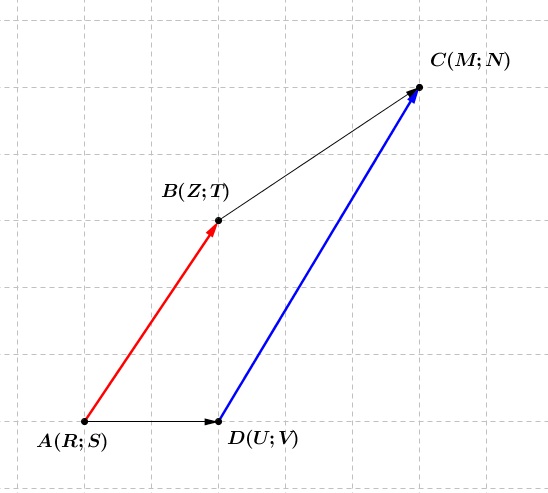
Bref, on doit vérifier que ExH-FxG=0 ET IxL-JxK=0 pour que le quadrilatère soit un parallélogramme, ok ?
Essaye maintenant, avec tout ce que je t'ai dit d'écrire l'algo en langage courant, comme ceci :
- Variables :
... //on déclare les 16 variables
-Initialisation:
... //on demande à l'utilisateur d'entrer les coordonnées des 4 pts + calcul des coordonnées des 4 vecteurs
-Traitement :
... //on fait le test avec une condition "si" et un opérateur boléen "et" car on doit vérifier que ExH-FxG=0 ET IxL-JxK=0
-Sortie :
//car dans le test on affichera un message disant si le quadrilatère est un parallélogramme ou non
à toi de jouer
Annuler
connectez vous