Inscription / Connexion Nouveau Sujet
DM algorithmique.
Bonjour, je vous mets la consigne :
f ets la fct définie sur l'intervalle [0;1] par :
f(x) = 1/(√(1+x2)
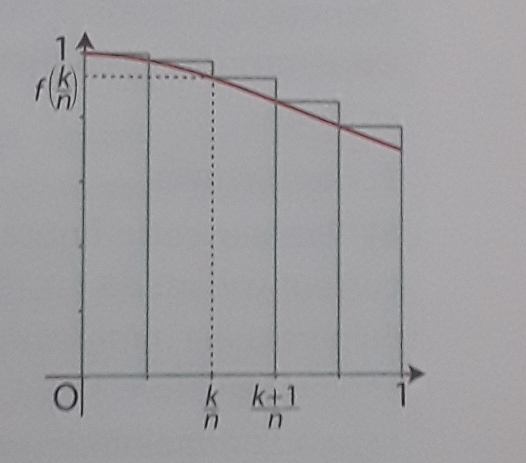
On subdivise l'intervalle [0;1] en n intervalles de longueur 1/n (n appartient à N*) et sur chaque intervalle [k/n;(k+1)/n] avec (0≤k≤n-1) on construit les rectangles de hauteur f(k/n).
On note Sn la somme des aires de ces rectangles et on admet que lim (n tend vers +infini) Sn existe et vaut l = 
10 f(x)dx.
Voici un algorithme incomplet permettant de déterminer une valeur approchée par excès de l.
Entrée
Saisir N (N appartient à N*)
Initialisations
X prend la valeur 0
S prend la valeur 0
H prend la valeur 1/N
Traitement
Pour k de 0 jusqu'à N-1
S prend la valeur S+...
X prend la valeur X+...
FinPour
S prend la valeur S x
Sortie
Afficher S
a) Compléter l'algorithme.
b) On saisit la valeur N=5. Quelle valeur obtiendra t-on en sortie?
c) Vérifier que la fonction F : x
ln(x+
(x2+1)) est une primitive sur [0;1] de f.
d) Calculer la valeur exacte de l.
Alors, je suis bloquée à la première question... Je sais que S correspond à la somme des aires. Mais, je ne vois pas ce que X peut-être.. L'intégrale? Mais, la question concernant la primitive de f(x) se pose en c)... Je n'y comprend plus rien!
Pouvez-vous me guider un tout petit peu, svp? Merci beaucoup!
Bonjour,
fais un schéma, n'importe quelle courbe fera l'affaire
sous la courbe et au dessus de l'axe Ox, dessine quelques rectangles dont l'angle supérieur droit est tangent à la courbe
Comment calcule -t-on l'aire d'un rectangle ?
la somme d'aires de rectangles ?
Attend, je ne sais pas si je peux y joindre l'image de la figure ou pas mais la voici (dites moi si non).
Aire d'un rectangle : Hauteur x largeur = f(k/n) x k/n ?
Somme d'aires de rectangle : n(f(k/n) x k/n) ?
En fait, non j'ai faux.
L'aire du rectangle est 1/n x f(k/n) = 1/n x 1/(√(1+(k/n)2) = 1/n+k
(vraiment désolée pour le double post mais comme il n'existe pas d'option de edit donc...)
non, tu ne peux pas simplifier comme cela
chaque rectangle doit voir son aire calculée individuellement
avec la formulation complète, mais l'algo va faire ça pourtoi...
donc il est nécessaire de compléter l'algo avec la formule
pour qu'il puisse calculer la valeur de chaque aire et faire la somme des aires
(sur le schéma fourni, par excès)
en b) n=5 ,donc 5 rectangles
tu dois formuler et calculer les aires et leur somme sans l'algo
Je vois, il faut que j'écris la formule complète. Mais, je ne comprend pas ce que S et X signifient et je comprend encore moins comment calculer la somme des aires de rectangles (j'en suis sûre que celle que j'ai dit précédemment est fausse).
Lorsque n = 5, alors 1/5 x 1/(√(1+(k/5)2) avec k allant de 0 jusqu'à 5-1=4.
Donc, pour k=0 c 0,2 ; k=1 c 0,196 ; k=2 c 0,186 ; k=3 c 0,171 ; k=4 c 0,156
C bon?
Qu'est ce qui est bon ?
Tu penses sérieusement qu'au bac, on veut que tu fasses des opérations ?
Non, tu doit donner des noms à tes aires,
tu dois écrire des égalités, montrer tes calculs, le résultat numérique on s'en f...
A5=1/5 x 1/(√(1+(0/5)2) = 0,2 lorsque k=0
A5=1/5 x 1/(√(1+(1/5)2) 
0,196 lorsque k=1
A5=1/5 x 1/(√(1+(2/5)2) 0,186 lorsque k=2
A5=1/5 x 1/(√(1+(3/5)2) 0,171 lorsque k=3
A5=1/5 x 1/(√(1+(4/5)2) 0,156 lorsque k=4
S5 = 0,2+0,196+0,186+0,171+0,156 0,909
Salut
Ce qu'il faut voir dans cet algo à compléter est surtout la variable S qui est une variable cumulative (elle regroupe la somme des aires des rectangles)
On écrira que pour k compris entre 1 et n-1
S=S + (1/n)*..... A toi
salut,
"je ne vois pas ce que X peut etre" En effet !
Consultation facultative de la resolution de l'exercice avec Xcas 
Entrée
Saisir N (N appartient à N*)
Initialisations
X prend la valeur 0
S prend la valeur 0
H prend la valeur 1/N
Traitement
Pour k de 0 jusqu'à N-1
S prend la valeur S+(1/1+X2)
X prend la valeur X+H
FinPour
S prend la valeur S x H
Sortie
Afficher S
Je trouve ça... Vous pensez que c'ets bon?
Annuler
connectez vous