Inscription / Connexion Nouveau Sujet
Dm de math : equation d'une asymptote oblique et dérivée.
Bonjours tout le monde !
Alors voilà, j'ai un petit problème de math..
ma fonction de départ est f(x) = x3 / (x-1)²
Ma premiere question est de trouver une asymptote oblique à f(x), en calculant les reels a, b, c et d pour que f(x) = ax + b + (cx+d)/(x-1)²
ça je crois que j'y suis arrivée :
[ax(x-1)²+b(x-1)²+cx+d]/(x-1)²
= [ax(x²-2x+1)+b(x²-2x+1)+cx+d)]/ (x-1)²
= [ax3-2ax²+ax+bx²-2bx+b+cx+d)]/(x-1)²
= [ax3+x²(b-2a)+x(a-2b+c)+b+d]/(x-1)²
par identification,
a=1
b-2a=0 <=> b=2a <=> b=2
a-2b+c=0 <=> c=2b-a <=> c=2*2-1 <=> c=4-1 <=> c=3
b+d=0 <=> d=-b <=> d = -2
donc f(x) = x+2+(3x-2)/(x-1)²
j'aimerais savoir si je ne me suis pas trompée, car lorsque je calcule la position de l'asymptote par rapport à la courbe ( asymptote y=x+2) ; je trouve
f(x)-(ax+b) = (3x-2)/(x-1)²
donc c'est du signe de 3x-2 ; d'ou la courbe coupe l'asymptote en x=2/3...
Or je sais pas, mais je pensais qu'une asymptote était comme une tangente... Donc qu'elle ne coupait pas la courbe !!
Puis ensuite je galère pour ma dérivée... Mais j'aimerai savoir si cette question est bonne avant :p
Quelqu'un pourrait m'aider s'il vous plait 
:)
bonjour,
dans ce genre de situation, trace la courbe et l'asymptote que tu as trouvee.
et regarde si cela a un sens...
ici ta courbe et ton asymptote donnent:
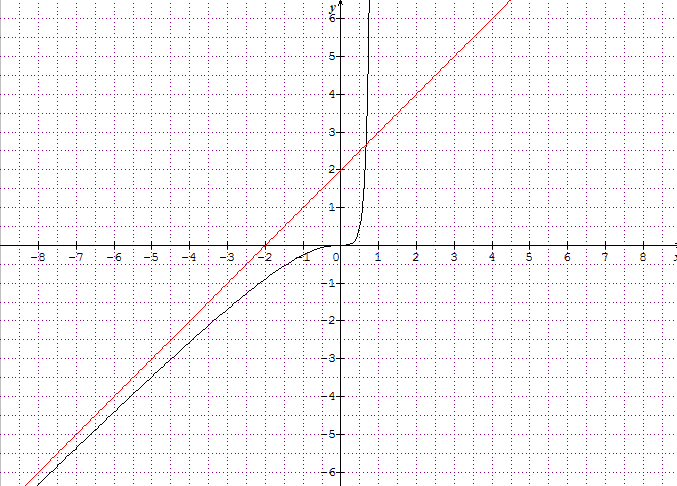
qu' en penses tu ? 
Je pense que ça a un sens...j'avais déjà tracé la courbe sur ma calculette, mais je me demandais si c'était normal qu'une asymptote coupe sa courbe ?
merci :d
donc voilà j'ai essayé de calculer ma dérivée avec f(x)=x+2+(3x-2)/(x-1)² mais ça me faisais des trucs improbables... Et comme je suis pas douée pour les dérivée j'ai décidé de la calculer à partir de f(x)= x3/ (x-1)²
en utilisant la formule
u/v = u'v-uv'/v²
ici u= x3 et u'=3x
v= (x-1)² et v'=2(x-1) * 1= 2(x-1)= 2x-2
D'ou f'(x) = [3x(x-1)²-x3(2x-2) ] / (x-1)4
= [3x(x²-2x+1)-(2x4-2x3)]/(x-1)4
= [3x3-3x²+3x-2x4-2x3] / (x-1)4
= [-2x4+x3-3x2+3x]/(x-1)4
Voilà ma dérivée... Mais elle est trop longue, j'ai essayé de la factoriser par (x-1) histoire d'enlever un peu de puissance mais j'y arrive pas :s c'est normal d'arriver à quelque chose d'aussi long ? !!
parce que ça va etre galère pour le tableau de signes !!
lol je t'arrete tout de suite :
u(x) = x³ donc u'(x) = 3x²
puis laisse v'(x) sous la forme 2(x-1) ce qui te permettra de factoriser le numerateur par (x-1) et de simplifier tout de suite .
essaie, si tu ne trouves pas, je te poste le resultat
Ah ben oui si je fais une faute desuite...
Alors je trouve :
f'(x) = [3x²(x-1)²-x3* 2 * (x-1) ] / (x-1)4
= [ (x-1) * [ 3x²(x-1)-2x3 ]] / (x-1)4
= [3x²(x-1)-2x3]/(x-1)3
= [3x3-3x²-2x3] / (x-1)3
= [x3-3x²]/(x-1)3
Ouii forcément là c'est plus simple lol
Mercii beaucoup de ton aide :)
normalement je ne devrais plus avoir de problèmes... Normalement 
Merci encore !!
Ah j'ai un probleme 
dans une question qui suit, on me demande de trouver une equation de la tangente T2 parallèle à la droite déquation y=x+2
donc de trouver une tangente à la courbe dont le coefficient directeur serait 1
du coup, je me suis dis que je devais faire f'(x)=1...
maiis problème : 1 est valeur interdite.
Comment la trouver ?
vite avant de partir...
1 est valeur interdite veut dire que tu ne peux pas calculer f(1)
mais tu peux resoudre f'(x) = 1
je reviens ce soir pour la suite, sinon un autre correcteur viendra t'aider entre temps
olala il faut que j'arrete avec mes question débiles lol, f'(x)=1 ça fait f'(1/3)=1
il faut donc calculer la tangente au point a=1/3; f(1/3)=1/12
y=f'(a)(x-a)+f(a)
donc au final ma tangente au point 1/3 est y=x-5/12
c'est bien cela ?
Bon j'arrive à la 7eme et dernière question de ma partie A...
la, cela doit etre facile, je ne comprend juste pas la question ^^ Apres avoir calculer les limites, la dérivée, le tableau de variation, 3 tangentes (y=x+2; y=0 et y=x-1/4)... On me demande ceci : Trouver grapiquement, selon les valeurs du réel m, le nombre de solutions de l'equation x3-mx²+2mx-m=0
Cela veut dire que je dois entrer ma fonction selon m? c'est à dire que je trace x3-x²+2x-1 pour m=1; et que je regarde combien de fois elle coupe l'axe des absisses ? Et que je fasse pareil pour par exemple -2 -1 0 1 2 3 4 5 ? En plus il faut juste ecrire le nombre de solutions..
Enfin cette question me parait bizzare lol, si quelqu'un pouvait m'éclairer...!!!
x3 - mx2 + 2mx - m = 0
x3 - m(x-1)2 = 0
x3 = m(x-1)2
x3/(x-1)2 = m
soit f(x) = m (m réel)
les solutions sont donc l'intersection de la courbe de f(x) et de la droite horizontale y = m.
Pour trouver le nombre de solutions, tu prends ta règle tu la glisse sur l'axe des ordonnées et parallèlement à l'axe des abscisses. tu regardes ainsi combien de fois elle coupe la courbe.
re bonsoir
Ouii mais concretement, je dois donner le nombre de solutions pour disons environ 10 chiffres differents ?
ah non, c'est bon, je peux dire que on voit qu'il commence à y avoir plusieurs solution à partir de m=6.75 c'est le "minimum de la seconde partie de la fonction". et ensuite il y a 3 solutions. Non ?
Oh, je crois qu'on est allé un peu vite...
Ne faut il pas essayer des nombres au hasard, pour ensuite voir qu'au bout d'un moment la droite coupe 3 fois y=0?
car voici ma partie B:
Soit g la fonction définie sur R par g(x)= x3-3x²+6x-3
1) démonter que l'équation g(x)=0 admet une et une seule solution 
dans l'intervalle [1/2 ; 2]
---> Bon la j'avais utilisé la solution d'Abdel, comme 3<6.75, g(x) admet une et une seule solution... mais ce n'est pas vraiment une démontration ?
enfin j'ai ecrit :
x3-3x²+6x-3=0
x3-3(x-1)²=0
x3=3(x-1)²
3=x3/(x-1)²
donc m=3
2) Donner un encadrement d'amplitude 10-2 de cette solution
----> faut-il utiliser la calculette ??
3) En déduire que sur l'intervalle [1/2 ; 2], la courbe C de la partie a coupe une et une seule fois la droite d'equation y=3
------> et là je pense qu'il faut mettre la démonstration d'Abdel ... Non?
Merci d'avance !!
abdel ne semble pas en ligne, je reprends le sujet alors...
non il faut faire comme il a dit ,et discuter en fonction des valeurs de m l'intersection de la courbe et de la droite y = m
pour la partie B:
1)là tu fais comme si tu ne connaissais pas la partie A.
tu etudies ta fonction et tu utilises le Theoreme des valeurs intermediaires
2) oui à la calculette
3) là tu fais le lien avec la partie A, comme tu l'as demontré ( en trouvant m = 3)
bon alors pour le 1), je trouve :
g'(x)=3x²-6x+6
= -36 ; <0 donc la fonction g'(x) n'est jamais égale à 0. elle est du signe de a=3, donc strictement positive.
g(x) est strictement croissante sur 
, car sa dérivée est strictement positive sur .
On peut donc utiliser le théoreme des valeurs intermédiaires, car g(x) est strictement continue(car dérivable) et croissante sur un intervalle et donc sur [1/2;2].
elle réalise donc une bijection de [1/2;2] dans [f(1/2),f(2)]=[-5/8;5]
0
[-5/8;5] donc 0 admet un antécédent unique, [0;5] ou encore l'equation g(x)=0 admet une solution unique à [0;5]
je ne me suis pas encore bien accoutumée aux bijection etc, vu qu'on l'a fait il y a une semaine, mais je pense que ça doit etre cela
= appartient à, je n'ai pas trouvé le vrai signe
c'est parfait !
(sauf le strictement continue c'est: continue car dérivable et strcitement croissante) )
Ok merci beaucoup!
Franchement je ne sais pas ce que j'aurais fait sans vous lol, j'y serais surement pas arrivée !! Certainement même
En plus, c'est le premier forum ou on envoie pas balader ceux qui posent des questions du style : réfléchi pour une fois lol...
Enfin bref :) merci beaucoup beaucoup beaucoup à toi à a Abdel 
:D
mais de rien Camille !
C'est un plaisir quand la personne cherche aussi de son coté
à bientôt peut être !
Bjr à tous,
Je viens de faire cet exo ... et je me rend compte que je n'ai pas bien saisi la question 7 de la partie A...
Normalment le calcul n'est pas necessaire puisqu'il demande graphiquement nan ?
Ah et j'ai pas bien compris non plus la question 3 de la partie B....
si vous pouviez me réexpliquer... merci d'avance !!!
Annuler
connectez vous