Salut,

Tu dois mettre le sujet en entier, si tu veux de l'aide.
Les personnes qui interviennent ici n'ont pas à sisposition tous les bouquins de maths de lycée et collège...  

Ah j'ai oublier de préciser que pour voir l'exercice il faut écrire dans la barre de recherche google "Sésamath 1ère S" vous cliquez ensuite sur le premier onglet qui est " Manuel sésamath en ligne - Sésamath" et vous aurez accès à tout le livre.
Cordialement.

Cela ne change en rien mon commentaire précédent, c'est la politique de ce site :

Le sujet :
On considère la fonction définie sur [0;4] par f(x)= Vx ( fonction racine carrée)
On Note C sa courbe représentative dans un repère orthonormé.
On note A le point de C d'abscisse 4.
Soit x un réel de [0;4], on note M le point de C d'abscisse x et N le point de [OA] d'abscisse x.

Y'a la figure que je ne peux vous diffuser.
***Tilk_11 >Figure récupérée***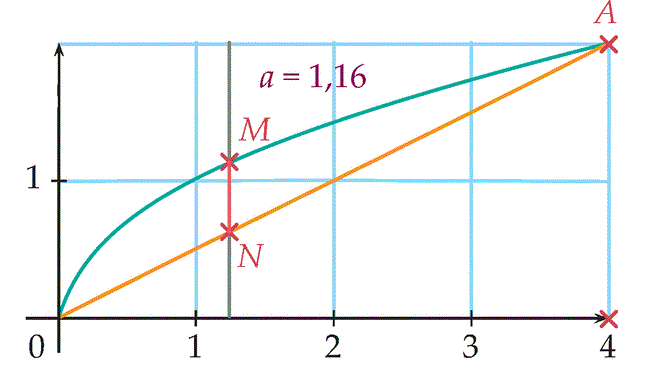


Partie A:
1) Construire cette figure sur un logiciel de géométrie dynamique
2)Afficher la longueur MN. Quelle semble être la position de M pour laquelle cette distance est maximale ? On note m cette distance maximale.
3) Pour tout réel de x de [0;4], on pose :
MN= f(x)
Montrer  que f(x) = Vx (racine carrée)-1/2x
4) Pour tout réel x de [0;4], montrer que f(x)-m<= ( Supérieur ou égal) à 0
Démontrer la conjecture du 1)

PARTIE B:
1) Construire, sur le logiciel, le triangle OMN et afficher son aire. Pour quelle valeur de x non nulle, arrondie au centième, le triangle OMN semble t-il isocèle en N ?
2) Résoudre algébriquement ce problème.
3)Montrer que l'unique solution x0 peut s'exprimer en fonction du nombre d'or = 1 +V5/2.

Merci d'avance à ceux qui m'aideront.

Aidez-moi svp..

Bonjour, moi aussi j'ai ce dm à rendre mais je n'arrive pas à faire la partie B quelqu'un pourrait m'aider svp !

Bonjour,

Oui et ?

D'accord merci mais c'est ON et pas AN

oui faute de frappe, (vu que j'ai bien dit calculer ON !)
ce qui ne change rien à rien sur la façon de procéder.

Bonjour,

Même avec vaut indications je n'arrive pas au 2) partie B pourrais-je avoir plus d'information

Merci d'avance

tu as les coordonnées de N et de M "en fonction de x" (les questions d'avant)

dont tu as la mesure de MN en fonction de x (la question d'avant : MN = x - 1/2x, donnée dans l'énoncé)

et tu peux calculer de la même façon la mesure de ON en fonction de x [...]

on veut que ces deux mesures, de MN et de ON, soient égales (triangle isocèle en N)

donc on l'écrit que ces deux expressions en fonction de x sont égales
cela donne une équation en l'inconnue x :
x - 1/2x = [...]

mais comme tu n'as rigoureusement rien écrit ici, je ne te la donnerais pas
(ce n'est pas à nous de faire les exos, on ne propose que de l'aide
cela veut dire donner des indices et des pistes, des choses à faire, et corriger ce qui est faux etc
pas des solutions toutes cuites)

du coup l'équation c'est la longueur MN de chaque coté du signe égal ???!

???
d'un coté c'est la longueur MN
et de l'autre la longueur ON pardi !!

Ouais bon je comprends pas l'alors comment on trouve ON merci quand meme

J'ai MN=  sqrt(x) - 1/2x

J'ai voulu calculer ON en trouvant l'équation de la droite  [OA] j'ai trouver 1/2x
donc en je fais MN=ON
donc sqrt(x) - 1/2x = 1/2x  ?

ou mon raisonnement est faux ?

l'équation de (OA) a été déja utilisée pour trouver question d'avant les coordonnées de N
(deja dit que tu connais les coordonnées de N)

ON s'obtient par la formule bien connue à partir des coordonnées de O (0; 0) et de N (x; 1/2x)

et ce n'est certainement pas 1/2x (qui est HN sur la figure complétée ainsi :

est ce que l'équation serait x-1/2x=x+1/2x

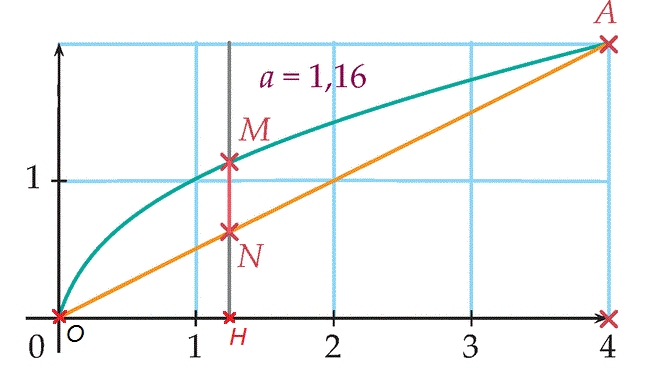
tu ne sais pas ton cours.

formule de la distance entre deux points : rappel de cours là Repère, coordonnées, milieu, longueur d'un segment

ok.

Donc avec la formule pour calculer un segment ON = sqrt (x_N-x_O)² + (y_N-y_O)²

Donc
ON = sqrt (x-0)² + (1/2x-0)²

oui mais :
ne pas oublier les parenthèses obligatoires pour dire jusqu'où va le radical
sinon il va "au plus court" et ne contient que le premier terme

ON = sqrt((x-0)² + (1/2x-0)²)

et puis il faudrait peut être développer et simplifier tout ça ... "moins 0" pfff

Ducoup ON est égal à 3/2x ?
Si cela est fauxje mettrais mon développement pourque mon m'aide a située l'erreur

oui, c'est faux

la racine carré d'une somme n'est pas la somme des racines carrées !!

ON= sqrt3/2[sup][/sup] mais apres comment procède pour supprimer justement le carré

ON est-il égal à sqrt(x² + x²/4) ?

Comment as tu fais pour trouver ce résultat cela t'embête de mettre ton developpement stp

OH = x, HN = x/2 et Pythagore ou formule de distance appliquée à la lettre
HN par Thalès ou équation de la droite (OA) ou question d'avant vu qu'on avait déja besoin de l'ordonnée de N

ON est-il égal à sqrt(x² + x²/4) ? oui
mais ça se simplifie
et 1 + 1/4 ne fait pas 3/4 !
ensuite la racine carrée d'un produit/quotient est bien le produit/quotient des racines carrés
c'est pour les sommes/différences que ça ne marche pas.

et le bouton X² ne sert pas à écrire "X²" mais à mettre ce qu'on veut en exposant (de ce qu'on veut) truc^blabla
exactement de la même façon que le bouton S sert à souligner ce qu'on veut, ce qu'on met (en le tapant) entre les balises
ici il faut donc écrire x[sup]2[/sup] dans la zone de saisie (les balises seules sont générées par le bouton) pour avoir x² dans le message publié
dès que le message est plus long qu'une demi-phrase en texte pur, il est fortement recommandé d'utiliser le bouton Aperçu avant de poster pour vérifier ce rendu et autres erreurs de frappe.

ON= 5/4^x2

l'absence de parenthèses et l'incompréhension de ce que j'ai dit à propos du bouton X² (en plus j'ai écrit exactement comment s'écrivait x² !! faut pas pousser !) et di bouton "Aperçu" fait qu'il est impossible de savoir si c'est juste ou faux.

ON= sqrt(x_n-x_o)²+(y_n-y_o)²
ON=sqrt((x-0)²+(1/2x-0)²)
ON=sqrt(x²+1/4x²)
ON=sqrt5/4x²

Est ce que mon développement est correct?

oui avec quelsqe parebthèss oubliées

ton déveloippelebr serait cvore t si t avais écrit

ON= sqrt((x_n-x_o)²+(y_n-y_o)²)
ON=sqrt((x-0)²+(1/2x-0)²)
ON=sqrt(x²+1/4x²)
ON=sqrt(5/4x²)

il faut continuer et simplifier : sqt(5/4x²) = sqrt(5)/sqrt(4) * sqrt(x²) = ...

puis ensuite ne pas perdre de vue pourquoi on a calculé ça ...

Donc si je comprends bien la version simplifier serait 5/2*x
Et cela nous sert pour trouver la question 3 non ?

oui. mais n'anticipons pas
déja pour terminer la question 2 car pour l'instant on en est là

résoudre x - 1/2x = [...] (MN = 0N)
dont on sait maintenant que c'est
x - 1/2x = x5/2
ou pour éviter des confusions en mettant les points sur les i (en ajoutant des parenthèses inutiles "de précaution") :
(x) - (1/2)x = x(5)/2

Mtn il faut mettre tous d'un seul côté non ou enlever les racines carré ?

déja tu as des x "ordinaires"

tu les regroupes ensemble

après pour les racines on verra

et je te conseille de poser directement phi = (1+5)/2
ce sera plus facile à écrire et ... ça anticipe sur la question d'après.

Pk phi ? Et toi pk les x on disparu ?

Pk ?? (SMS interdit, tu voulais dire pourquoi" ?) pourquoi pas, c'est juste une simplification d'écriture d'une valeur numérique un peu trop longue à écrire répétée tout au long des calculs

pk les x on disparu ?

tu ne sais pas suivre un plan global et il faut qu'on te fasse une seule mini étape par message ? on n'est pas rendu ...

je parle de ceux là :

(x) - (1/2)x = x(5)/2

à regrouper ensemble.

Ok doncx

Ok doncx =(1+5)/2 x

oui;
et maintenant tu le vois mon "phi pour simplifier l'écriture"

x = phi*x = phi(x)² etc

Oui merci je vois maintenant

Mais après il faut supprimer ces racines carré et le x pour pouvoir répondre à la question 3 non?

il ne faut pas "supprimer le x" mais résoudre cette équation en x

c'est à dire aboutir à x = une certaine valeur numérique que tu peux écrire en valeur exacte (avec des racines de 5 écrites racine de 5), puis en valeur numérique approchée (calculette) pour faire bonne mesure.
ou dans la question suivante "en fonction de phi", parce que le nombre d'or c'est justement mon "phi"

en tout cas pour résoudre cette équation avec des racines carrées de x il faut utiliser le fait que
A = B

équivaut à
A = B² avec B positif (et A aussi vu que c'est le carré de B)

(par définition)

D'accord donc les résultats final serait x=6/4x² et en simplifiant x=3/2x² ? Si cela est faux vous pourriez le corriger svp

n'importe quoi.

x en fonction de x lui-même tu appelles ça une valeur numérique toi ???
sais tu seulement ce que veut dire résoudre une équation, de manière générale ????


de plus tes développements sont faux
(A + B)² n'a jamais été égal à A² + B²

(1+5)² n'a jamais été égal à 1² + 5 = 6 !!

(de tout façon vaut mieux ne pas le développer, ça perd toute signification en rapport avec la question suivante)

Si À= B² sa veut dire qu'il faut mettre (1+5)/2x au carré non ?!

oui mais
- ton calcul de ce truc au carré est faux.
- et le laisser écrit ((1+5)/2)²x² sera bien plus malin.
(en termes de phi : phi²x² et on cherche donc à résoudre x = phi²x²)