Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Limites de fonctionsTopics traitant de Limites de fonctions [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Dm de math sur la fonction logarithme népérien.

Posté par
Kizmaa 27-12-12 à 17:34

Bonjour à tous,

J'ai un DM à faire, presque fini, mais j'ai besoin d'aide et d'avis d'expert, le voici :

On considère la fonction f définie sur [0;+[ par :
\[f(x) = \left\{\begin{array}{l l} \\   xln(1+\frac{1}{x²}) & \quad \mbox{si $x>0$}\\ \\   f(0) = 0 \end{array} \right. \]

On note (C) la courbe représentative de f dans un répère orthonormal (O;;) (unité graph : 5 cm)

A- Etude d'une fonction auxilaire

On considère la fonction g définie sur ]0;+[ par g(x) = ln(1+\frac{1}{x²})-\frac{2}{x²+1}.

1)a) Démontrer que, pour x ]0;+[, on a g'(x) = \frac{2(x²-1)}{x(x²+1)²}

Je calcul la dérivée de ln(1+\frac{1}{x²}), je trouve : \frac{-2}{x^3}.
De même pour -\frac{2}{x²+1}, je trouve : \frac{4x}{(x²+1)²}
Ensuite j'addition les deux, ce qui me fait g'(x) = \frac{-2}{x^3}+\frac{4x}{(x²+1)²}
Et là, j'ai tout essayé, factoriser, développer, etc .. après, je l'ai peut-être mal fait, mais j'arrive pas à trouver le résultat final.

b) Etudier le signe de g'(x) selon les valeurs de x :

J'ai g'(x) négative si x]O,1[ & positive si x ]1, +[

2) Etudier les limites de g en 0 et en + :
$\lim\limits_{x \to 0}$ f(x) = +
\lim_{x\to +\infty} f(x) = 0
J'épargne les détails, mais si je me trompe faites moi signe.

3)a) Dresser le tableau de variations de g.

b) En déduire qu'il existe un unique nombre réel > 0 tel que g() = 0 . Donner un encadrement de à 10^-2 près.
j'ai utilisé le théorème des valeurs intermédiaires et j'ai trouvé que appartient à l'intervalle ]O;1[, à l'aide de ma calculette, j'ai vérifié en calculant g(0,5) et g(0,6) qui sont respectivement positive et négative.
Et j'ai trouvé l'encadrement.

4) Déterminer le signe de g(x) sur l'intervalle ]0;+[
J'ai positif sur ]O;[ & négatif sur ];+[

B) Etude de la fonction f

1)  Montrer que pour x de ]0;+[, f'(x) = g(x). Et en déduire les variations de f sur ]0;+[.

J'ai dit que ln(1+\frac{1}{x²}) = ln(x²-1)-2lnx
J'ai ensuite calculé la dérivée de (ln(x²-1)-2lnx)'= \frac{-2}{x}(x²+1)
C'est de la forme u'v-uv', je fini par retrouver g(x) donc f'(x)=g(x).

Et comme f'(x)=g(x), elles ont le même signe donc je reprend donc les résultats de la partie A.

Je n'ai pas encore bien traité la suite, mais je vous met mes idées afin que vous puissiez les confirmer ou les modifier.

2)a) Etudier la limite de xf(x) lorsque x tend vers + linfini
(On pourra poser h = 1/x²)

On demande un changement de variable, cela reviens donc à calculer la limite du taux d'accroissement, donc
Avec le changement de variable xf(x) = (1/h) ln(1+h).
C'est là qu'on va utiliser la définition de la dérivée. La fonction qui à h associe ln(1+h) est dérivable et admet comme dérivée en 0 :
\lim_{h\to 0} \frac{ln(1+h)-0}{h-0}
Or la dérivée de ln(1+h) est \frac{1}{1+h} et qui vaut 1 en 0.

Donc \lim_{h\to 0} \frac{ln(1+h)}{h}=1 qui est bien la limite que l'on cherché après le changement de variable.

b) En déduire la limite de f(x) quand x tend vers +

Je trouve 0 au brouillon, mais je ne sais pas trop comment le rédiger, s'y vous pouviez m'aider, merci.

3) Etude de f en 0
a) Montrer que pour x > 0 , f(x) peut s'écrire sous la forme f(x) = xln(x²+1)-2xlnx sur ]0;+[, et utiiser cette écriture pour démontrer les continuitée de f en 0.

J'ai tout bêtement repris la question 1) de la partie B, j'ai dit que ln(1+\frac{1}{x²}) = ln(x²-1)-2lnx, en rajoutant un x devant, ce qui donnera xln(x²-1)-2lnx, après je détaillerai plus lors de la rédaction.

Pour la continuité je ne vois pas comment faire par contre ...

b) Etudier la dérivabilité de f en 0. Préciser la tangente à la courbe C au point O.

Je ne sais pas si il faut que j'utilise cette fonction f(x)=xln(x²-1)-2lnx ou celle-là f(x)=xln(1+\frac{1}{x²}) pour determiner la dérivabilité. Aidez moi s'il vous plaît.
Après il faut que j'applique l'équation de la tangente : T:y= f'(0)(x-0)+f(0).

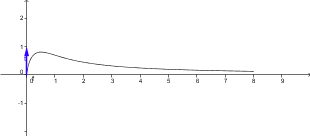
4) Dresser le tableau de variations de f. Tracer la courbe C. On prendra pour la valeur 0.5.

Ici, rien de compliqué, juste une petite synthèse du DM avec un tableau de variations, la courbe et f()=0.5

Voilà mon DM en entier, au final, j'ai juste besoin d'aide dans les questions : A-1)a) ; B-2)b) , 3)a) & 3)b).
Mais une petite vérification sur les autres questions m'aiderai à confirmer mes résultats.

Je vous remercie d'avance pour votre aide.

Cordialement,
Kizmaa.

Posté par
malou Webmasterre : Dm de math sur la fonction logarithme népérien. 27-12-12 à 17:41

Bonsoir

aide pour A 1 a
ta dérivée du ln est fausse

la dérivée de lnu est u'/u et tu as oublié le "/u"

sauf erreur, -2/x(x²+1)

Posté par
Kizmaare : Dm de math sur la fonction logarithme népérien. 28-12-12 à 11:33

En effet, petite erreur d'interprétation. Je te remercie malou .
Donc ça fait : \frac{-2}{x}(x²+1)+\frac{4x}{(x²+1)²}=\frac{(-2x²-2)}{x}+\frac{4x}{(x²+1)²}

Il faut mettre ceci au même dénominateur, mais je ne trouve pas quel dénominateur commun il pourrai y avoir ...

Posté par
malou Webmasterre : Dm de math sur la fonction logarithme népérien. 28-12-12 à 11:38

attention, la dérivée de ton log donne

\frac{-2}{x(x^2+1)}

et non ce que tu dis....

Posté par
Kizmaare : Dm de math sur la fonction logarithme népérien. 28-12-12 à 12:40

Mmmh, j'ai mal interprété que tu as dit : " -2/x(x²+1)".

Je vois, donc : \frac{-2}{x(x²+1)}+\frac{4x}{(x²+1)²}= \frac{-2(x²+1)+4x}{x(x²+1)²}=\frac{-2x²-2+4x}{x(x²+1)²}

Là, je vois pas trop, le 4x vient me déranger ...

Posté par
malou Webmasterre : Dm de math sur la fonction logarithme népérien. 28-12-12 à 13:15

deux remarques :
tu devrais calculer toi-même cette dérivée du ln pour comprendre, sans t'appuyer sur mon résultat...tu dois savoir faire ça....

ensuite : dans ta réduction au même dénominateur, tu as oublié de multiplier la 2e fraction par x (haut et bas) et donc cela te donne 4x² et non 4x
regarde un peu

Posté par
Kizmaare : Dm de math sur la fonction logarithme népérien. 28-12-12 à 15:23

J'ai compris la dérivation du ln, (ln(u))'= \frac{u'}{u}

ça donne donc : ln(1+\frac{1}{x²})=\frac{-2}{x^3}*\frac{x²}{(1+x²)}

Après simplification : \frac{-2}{x(x²+1)}

Voilà .

La dérivée : \frac{-2}{x(x²+1)}+\frac{4x}{(x²+1)²}=\frac{-2}{(1+x)²}(\frac{1}{x}+\frac{2}{(1+x)²})=(\frac{-2}{(1+x)²})\frac{1+x²+2x}{x(1+x²)}=\frac{-2(1+x²)}{x(1+x²)²}

Là c'est bon, normalement.

Maintenant, pourrai-je avoir de l'aide pour la B-2)b), 3)a) & 3)b) s'il vous plaît.

Posté par
malou Webmasterre : Dm de math sur la fonction logarithme népérien. 28-12-12 à 16:18

je regarde tout à l'heure !

Posté par
malou Webmasterre : Dm de math sur la fonction logarithme népérien. 28-12-12 à 17:52

pour la fct auxiliaire g, tes limites sont bonnes à l& question 2, mais tu as écrit f à la place de g

pour 3b
tu donnes bien un encadrement de , mais là, il est à 10^(-1) et non à 10^(-2) comme le demande l"énoncé

étude de f

Citation :
J'ai dit que ln(1+\frac{1}{x²}) = ln(x²-1)-2lnx

c'est faux, car tu devrais avoir ln(x^2+1)
revois un peu ce passage, je crois qu'hier tu étais fâchée avec les dérivées!....

Citation :
b) En déduire la limite de f(x) quand x tend vers +

Je trouve 0 au brouillon, mais je ne sais pas trop comment le rédiger, s'y vous pouviez m'aider, merci.

j'ai posé t=1/x² lorsque x tend vers + l'infini, t tend vers 0
et j'ai réussi à lever l'indétermination, je ne sais pas s'il y a plus simple

Citation :
Pour la continuité je ne vois pas comment faire par contre ...

tu dois démontrer que la limite qd x tend vers 0 (à droite) va valoir f(0)

voilà, regarde un peu tout ça....

Posté par
Kizmaare : Dm de math sur la fonction logarithme népérien. 28-12-12 à 21:31

Je m'occupe de ça ce soir, et je vous tiens au courant demain pour mes résultats.

Merci beaucoup pour la rapidité de vos réponses.

Posté par
malou Webmasterre : Dm de math sur la fonction logarithme népérien. 28-12-12 à 21:33

OK, pas de souci
je me connecte régulièrement

Posté par
Kizmaare : Dm de math sur la fonction logarithme népérien. 29-12-12 à 15:24

Bonjour,

B-1)

Citation :
c'est faux, car tu devrais avoir
revois un peu ce passage, je crois qu'hier tu étais fâchée avec les dérivées!....


C'était une erreur que j'ai faite sur mon brouillon, et que j'ai recopié par la suite ...
Aussi pour cette question, je me suis également trompé dans l'énoncé, il faut que je dise que f(x)=xln(x²+1)-2xln(x)

Donc j'ai fait ceci : xln(1+\frac{1}{x²}) = xln(\frac{x²+1}{x²}) = xln(x²+1)-xln(x)² = xln(x²+1)-2xln(x)

B-2)a)
Citation :
tu dois démontrer que la limite qd x tend vers 0 (à droite) va valoir f(0)

voilà, regarde un peu tout ça....


f(x) = xln(x²+1)-2xln(x)

\lim_{x\to 0 \atop} ln(x²+1) = ln(1) = 0  d'où  \lim_{x\to 0 \atop} xln(x²+1) = 0

\lim_{x\to 0 \atop x>0} ln(x) = -\infty d'où \lim_{x\to 0 \atop x>0} 2xln(x) = 0

Donc \lim_{x\to 0 \atop x>0} f(x) = 0

Or comme f(0) = 0 cela revient à calculer \lim_{x\to f(0) \atop x>f(0)} f(x) = 0
Donc f est continue.

Je ne suis vraiment pas sûr de moi ..

B-2)b)
Citation :
j'ai posé t=1/x² lorsque x tend vers + l'infini, t tend vers 0
et j'ai réussi à lever l'indétermination, je ne sais pas s'il y a plus simple


Cela me fait f(x)=xln(1+t)
Je ne comprend pas..

Posté par
malou Webmasterre : Dm de math sur la fonction logarithme népérien. 29-12-12 à 16:16

alors
OK pour le début

ensuite
ta limite Ok, sauf un passage que je n'aime pas

Citation :
\lim_{x\to 0 \atop} ln(x²+1) = ln(1) = 0 d'où \lim_{x\to 0 \atop} xln(x²+1) = 0


c'est le d'où qui me gêne (dis que c'est une forme du cours)

Citation :
Donc \lim_{x\to 0 \atop x>0} f(x) = 0


Ok, et écris mais f(0)=0 donc

\lim_{x\to 0 \atop x>0} f(x) = f(0)

donc f est continue en 0

pour B2b
quand on fait un changement de variable, il faut le faire complètement
donc tu ne dois plus avoir de x, mais que la lettre t

Posté par
malou Webmasterre : Dm de math sur la fonction logarithme népérien. 29-12-12 à 16:18

excuses !


bon, erreur dans mes recopies
cette limite là, le "d'où" est bon

c'est dans la suivante que ça va pas...

Citation :
\lim_{x\to 0 \atop x>0} ln(x) = -\infty d'où \lim_{x\to 0 \atop x>0} 2xln(x) = 0


c'est là, la forme du cours

Posté par
Kizmaare : Dm de math sur la fonction logarithme népérien. 29-12-12 à 16:45

Ok, j'ai compris pour le "d'où", qu'il faut que je remplace en disant que c'est une forme du cours.
Mais comment je peux formuler cela ? Car je n'aime pas dire "D'après le cours" dans mes copies, et les profs aussi ..

Citation :
pour B2b
quand on fait un changement de variable, il faut le faire complètement
donc tu ne dois plus avoir de x, mais que la lettre t


Ok, donc si t = \frac{1}{x²}.
ça donne f(x) = xln(1+t)

Je bloque pour remplacé le x sachant que t = \frac{1}{x²}.
J'ai dit que x² = \frac{1}{t} donc x = \sqrt\frac{1}{t}

Posté par
malou Webmasterre : Dm de math sur la fonction logarithme népérien. 29-12-12 à 16:50

je pense que c'est vraiment une forme du cours...non ?...ou alors, le prof vous a fait apprendre "que s l'emportait sur le log", je ne sais pas...regarde....

pour le changement de variable, oui, c'est ça

Citation :
x = \sqrt\frac{1}{t}


faut pas avoir peur...je crois qu'on va savoir chercher la limite, si je ne me suis pas trompée...

Posté par
Kizmaare : Dm de math sur la fonction logarithme népérien. 29-12-12 à 17:43

On a pas encore étudié le Log en math, que en Physique.
Je vais regarder.

Oui il me faut la limite de f(x) quand x tend vers +.

Avec le changement de variable on a la fonction suivante : f(x) = \sqrt \frac{1}{t}ln(1+t)

\lim_{t\to +\infty \atop} \frac{1}{t} = 0 d'où \lim_{t\to +\infty \atop} \sqrt\frac{1}{t} = 0

De plus \lim_{t\to +\infty \atop} ln(t) = +\infty donc \lim_{t\to +\infty \atop} ln(1+t) = +\infty

Donc \lim_{t\to +\infty \atop} \sqrt\frac{1}{t}ln(1+t) = 0 d'où \lim_{x\to +\infty \atop} f(x) = 0

La rédaction c'est pas mon fort dans les maths, mais j'ai le raisonnement. Ceci est juste ?

Posté par
malou Webmasterre : Dm de math sur la fonction logarithme népérien. 29-12-12 à 18:04

ben, non, pas vraiment
cela fera bien 0, mais pas démontré comme ça

attention, quand x tend vers +, t tend vers 0
mais si tu n'as pas encore étudié le log népérien, comment fais-tu ?

\lim_{t\to 0\atop} \sqrt\frac{1}{t}ln(1+t) =\lim_{t\to 0 \atop}\dfrac{ln(1+t)-ln1}{t}\times\sqrt{t}

on reconnait dans \lim_{t\to 0 \atop}\dfrac{ln(1+t)-ln1}{t}
le nombre dérivé de ln en 1, ce qui donne 1
et la racine de t tend vers 0
donc le produit fait O

Posté par
Kizmaare : Dm de math sur la fonction logarithme népérien. 29-12-12 à 18:21

Ok, donc ça revient à démontrer la limite du taux d'accroissement de la fonction.

Merci, j'ai bien compris mon erreur après l'avoir refais 3 fois.

Presque fini, j'aurai besoin d'aide ici :

Citation :
b) Etudier la dérivabilité de f en 0. Préciser la tangente à la courbe C au point O.

Je ne sais pas si il faut que j'utilise cette fonction  ou celle-là  pour determiner la dérivabilité. Aidez moi s'il vous plaît.
Après il faut que j'applique l'équation de la tangente : T:y= f'(0)(x-0)+f(0).


Je voudrai juste savoir quelle fonction de f faut-il que je choisisse pour calculer l'équation de T..
Celle-ci : f(x) = xln(x²+1)-xln(x)²
Ou celle-ci : f(x) = xln(1+\frac{1}{x²})

Merci

Posté par
Kizmaare : Dm de math sur la fonction logarithme népérien. 29-12-12 à 18:23

Erreur de ma part : la première c'est celle-ci : f(x) = xln(x²+1)-2xln(x)

Posté par
malou Webmasterre : Dm de math sur la fonction logarithme népérien. 29-12-12 à 18:24

pour calculer la dérivée en un point qcq autre que 0, tu prends une formule ou l'autre, peu importe cela reviendra au même

par contre en 0
tu vas devoir calculer [f(h)-f(0)]/h et regarder s'il y a une limite finie qd h tend vers 0+

Posté par
Kizmaare : Dm de math sur la fonction logarithme népérien. 29-12-12 à 18:34

Citation :
par contre en 0
tu vas devoir calculer [f(h)-f(0)]/h et regarder s'il y a une limite finie qd h tend vers 0+


Donc si la fonction admet une limite finie alors elle sera dérivable en ce point ?

Cela revient à faire : \frac{f(h)-f(0)}{h-0}

Je remplace f(h) par la fonction et f(0) de même. Mais la fonction f(h) c'est f(x) ?
Je calcul la limite du truc que j'obtiens, et si elle a une limite finie quand h tend vers 0, alors elle est dérivable.
Et je calcul ensuite l'équation de la Tangente T au point O.

Je me trompe ?

J'ai trouvé ceci pour m'inspirer un peu : https://www.ilemaths.net/forum-sujet-143649-2.html

Posté par
malou Webmasterre : Dm de math sur la fonction logarithme népérien. 29-12-12 à 18:39

oui, c'est bien ça

\[f(x) = \left\{\begin{array}{l l} \\ xln(1+\frac{1}{x²}) & \quad \mbox{si $x>0$}\\ \\ f(0) = 0 \end{array} \right. \]

\dfrac{f(h)-0}{h}=\dfrac{hln(1+\frac{1}{h²})}{h}=ln(1+\frac{1}{h²})

et lorsque h tend vers 0, cette limite est infinie

on dit que la courbe admet une tangente portée par l'axe des ordonnées

OK ?

Posté par
Kizmaare : Dm de math sur la fonction logarithme népérien. 29-12-12 à 18:51

Ok, mais lorsque l'on me dit "étudier la dérivabilité de f en 0".

Je fait les calculs préliminaires, et je dit que lorsque h tend vers 0, cette limite est infinie, cela veux dire que la fonction n'est pas dérivable en 0 mais est dérivable en l'infinie ?

Je comprend pas trop la signification de "portée" dans le contexte..

Posté par
malou Webmasterre : Dm de math sur la fonction logarithme népérien. 29-12-12 à 19:00

Citation :
Je fait les calculs préliminaires, et je dit que lorsque h tend vers 0, cette limite est infinie, cela veux dire que la fonction n'est pas dérivable en 0


ça c'est bon
elle n'est donc pas dérivable en 0 (donc pas de coeff directeur fini pour une tangente)

sauf que cette limite est infinie, donc cela revient à dire que la droite sécante qui devient tangente a un coeff directeur qui tend vers + l'infini, et ça, ça donne une droite parallèle à l'axe des ordonnées

et comme la courbe passe par l'origine, cette parallèle à l'axe des ordonnées est tout simplement l'axe des ordonnées lui-même

regarde

Dm de math sur la fonction logarithme népérien.

Posté par
Kizmaare : Dm de math sur la fonction logarithme népérien. 29-12-12 à 19:35

D'accord, j'ai compris.

Donc la tangente n'admet pas d'équation de la forme y= ax+b.
J'ai essayé de calculer l'équation de la tangente mais j'en est déduit que ce n'était pas possible, car f'(0) n'est pas calculable car la division par 0 est impossible..

Posté par
malou Webmasterre : Dm de math sur la fonction logarithme népérien. 29-12-12 à 19:57

voilà, très bien vu

effectivement ce sont des droites dont l'équation ne peut pas s'écrire y=ax+b

elles s'écrivent "x=a" avec a constante, (droite parallèle à l'axe des ordonnées)

Posté par
Kizmaare : Dm de math sur la fonction logarithme népérien. 29-12-12 à 20:12

Oui voilà, en l'occurence ici x=0.

J'ai compris.

Place à la rédaction maintenant.
Je rédige, et je vous tiens au courant mardi soir si j'ai des problèmes ou autres.
Avant je ne pourrai, entre les fêtes etc ..

Je vous remercie beaucoup, ça ma vraiment aidé.

Bonne soirée et bonne année.

Cordialement,
Kizmaa.

Posté par
malou Webmasterre : Dm de math sur la fonction logarithme népérien. 29-12-12 à 20:13

OK, bonne suite de vacances!....à + si besoin !
Bonnes fêtes de fin d'année à toi aussi!

Posté par
Kizmaare : Dm de math sur la fonction logarithme népérien. 04-01-13 à 12:21

Bonjour,

J'ai un petit probleme lors de la redaction pour B-2)a)

Donc j'ai la limite du taux d'accroisement qui vaut 1 quand h tend vers 0.
Mais je dois trouver la limite de xf(x) quand x tend vers +infini. Et celle-ci vaut 0 ?

Merci

Posté par
malou Webmasterre : Dm de math sur la fonction logarithme népérien. 04-01-13 à 17:28

Citation :
Mais je dois trouver la limite de xf(x) quand x tend vers +infini. Et celle-ci vaut 0 ?


non, je pense que ça vaut 1

cela donne x²ln(1+1/x²)=\dfrac{ln(1+\frac{1}{x^2})}{\frac{1}{x^2}} \\ \\ = \dfrac{ln(1+h)}{h}

et ça ça tend vers 1 lorsque h tend vers 0, non ?

Posté par
Kizmaare : Dm de math sur la fonction logarithme népérien. 05-01-13 à 10:55

Oui normalement oui, mais j'avais un doute.

Quand x tend vers +infini, cela équivaut à h quand il tend vers 0, donc la limite est 1.

Et aussi pour A-2), les limites de g en +inf et 0, donc j'ai trouvé que ça fesait 0 en +inf et +inf en 0 ..

Pour trouver le resultats final, j'y arrive, mais pour le détail des calcul, je ne sais pas quoi mettre..

Posté par
malou Webmasterre : Dm de math sur la fonction logarithme népérien. 05-01-13 à 11:16

g(x) = ln(1+\frac{1}{x²})-\frac{2}{x²+1}.

oui, pour tes limites, sur ta copie, décompose

en + l'infini
\frac{1}{x²} tend vers 0
1+\frac{1}{x²} tend vers 1
ln(1+\frac{1}{x²}) tend donc vers 0

etc....
tu ne rencontres pas de FI, ça va passer tout seul

Posté par
Kizmaare : Dm de math sur la fonction logarithme népérien. 05-01-13 à 17:09

Et -\frac{2}{x²+1} est négligeable ? Où je dit quand même qu'en + il tend vers 0 ?

Posté par
Kizmaare : Dm de math sur la fonction logarithme népérien. 05-01-13 à 17:13

Enfin quand x tend vers +, -\frac{2}{x²+1} tend vers 0

Posté par
malou Webmasterre : Dm de math sur la fonction logarithme népérien. 05-01-13 à 17:13

tu dis qu'il tend vers 0

Posté par
Kizmaare : Dm de math sur la fonction logarithme népérien. 05-01-13 à 18:32

Ok merci beaucoup.


Rechercher
Menu
Espace membre
12 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1720 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !