Inscription / Connexion Nouveau Sujet
Dm de maths
Bonjour,
J'ai un DM pour le 19 Avril Mais je n'arrive pas à résoudre un exercice sur les vecteurs. J'aurai donc besoins de votre aide svp .
Le plan est rapporté au repère orthonormé (O, 
,
On considère les points A(2;5/2), B(6;9/2) et C(3;3/2)
1- Placer les points dans le plan.
2- Montrer que le triangle ABC est rectangle.
3- Déterminer les coordonnées du point D image du point C par la translation du vecteur 
où (2;0).
4-Soit E le milieu du segment [AB]. Calculer les coordonnées de E.
5- Soit F le point tel que vecteur EF= vecteur DE. Quelle est la nature du quadrilatère ADBF ?
6-Démontrer que les points A,B,C,D et F appartiennent à un même cercle dont on déterminera le centre et le rayon.
Merci d'avance & bonne journée.
Qu'as-tu comme feuille?
Feuille à grands carreaux
Si tu prends un carreau =1 alors 5/2 = 5 carreaux et demi
Feuille à petits carreaux
Si tu prends 2 carreaux =1 alors 5/2 = 5 petits carreaux
Excuse-moi, j'ai fait une erreur.
Feuille à grands carreaux
Si tu prends un carreau =1 alors 5/2 = 2 carreaux et demi
Feuille à petits carreaux
Si tu prends 2 carreaux =1 alors 5/2 = 5 petits carreaux
Bon, visiblement tu utilises un papier millimétré.
5/2 correspond à 2,5 ; 9/2 à 4,5 et 3/2 à 1,5
Je te fais le schéma pour la peine:
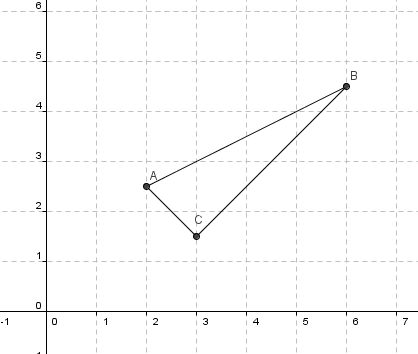
tu peux remarquer que ABC est rectangle en C
Tu utilises la réciproque du théorème de Pythagore : Si dans un triangle, la somme des carrés de deux côtés est égale au carré du plus grand côté, alors ce triangle est rectangle.
Donc si AC² + CB² = AB² alors ABC est rectangle en C
Mais tu as les coordonnées donc tu peux calculer les distances
Je te conseille fortement d'ouvrir tes cours et de les poser devant toi, la formule te permettant de les calculer s'y trouve surement.
4.47Dans le triagle ABC ,
(
2)² + (18)² = 2+18 = 20
AB² = (20)² = 20
D'après la réciproque du th de pyth,le triangle ABC est rectangle en C
Oui. 
Explique bien les étapes dans ton raisonnement.
Donc
Par conséquent, d'après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en C.
Pour la suite, tu y arrives?
3- Déterminer les coordonnées du point D image du point C par la translation du vecteur où (2;0).
"D image du point C par la translation du vecteur où (2;0)".
Cela veut dire que donc a pour coordonnées (2;0)
Or les coordonnées de sont
soit
D'où:
Fais le calcul...
Petite erreur de copié collé, tu dois retirer quelques "" superflues.
Cela veut dire que donc
a pour coordonnées (2;0)
Or les coordonnées de sont
soit
Pour le 4)
As-tu ouvert ton cours devant toi?
La formule pour calculer les coordonnées du milieu d'un segment doit y être.
Oui ,
Formule :
soit I le milieu de [AB]
A(Xa ; Ya)
B(Xb ; Yb)
alors les coordonnées de I sont ( (Xa+Xb)/2 ; (Ya+Yb)/2 )
Donc soit E le milieu de [AB]
A(Xa ; Ya)
B(Xb ; Yb)
D'où :
A(2;5/2)
B(6;9/2)
les coordonnées de E sont ( (Xa+Xb)/2 ; (Ya+Yb)/2 )
D'où :
E ((2+6)/2) ; (5/2;9/2/2)
E(8/2) ; (7/2)
E(4;3.5)
Techniquement, F
à la droite (DE) donc tu traces la droite (DE) et tu places le point F à la même distance de E que E de D (E est donc le milieu de [FD]
j'ai un peu de mal à voir mais ça a l'air bon.
Tu sais donc que E est le milieu de [AB]et que E est le milieu de [FD].
Que peux-tu dire tout de suite sur ADBF?
C'est un carrée car les diagonales se coupent en leur milieu
C'est un carré, oui, mais le fait que les diagonales se coupent en leur milieu ne montre que le fait que ADBF est un parallélogramme (ce qui est déjà un bon début).
Maintenant,
soit tu montres que les diagonales sont perpendiculaires et de même longueur,
soit tu montres que 1 des angles est droit (par exemple que:
Si un quadrilatère est un carré, alors ses diagonales sont perpendiculaires.
Oui mais l'inverse n'est pas vrai.
par exemple, si un parallélogramme a ses diagonales perpendiculaires, il peut s'agir d'un carré mais aussi d'un losange.
Je vais devoir m'absenter, essaie, d'après ma réponse de 12:45, d'avancer, je corrigerai plus tard.
Annuler
connectez vous