Inscription / Connexion Nouveau Sujet
DM de maths , bloqué .
Bonjour ,
Je vous contacte car mon professeur de maths etant absent je ne peux pas le contacter pour me débloquer sur ce dm .
Voici le sujet :
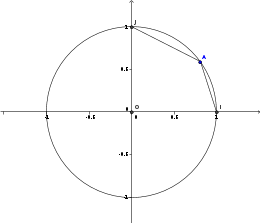
sur le cercle trigonométrique ci contre , le point A est le point asocié au réel pi/5
1) démontrer que les triangles OAJ et AJI sont isocèles
2) dans le triangle AIJ , H est le pied de la hauteur issue de A
Démontrer que HI = 1-cospi/5 et en déduire que :
OJ = 2cos pi/5 -1
3) Dans le triangle OAJ , L est le pied de la hauteur issue de J
démontrer que OJ = 1/ 2cospi/5
4)En déduire que (4cos²pi/5)-(2cospi/5)-1=0
Pour le moment , j'ai réussi a prouver que OAJ était isocèle , à faire HI = 1 - cospi/5 et la question 3 .
J'ai vraiment besoin d'aide , un des derniers dm de l'année qui doit etre excellent .
Merci d'avance pour l'aide ! 
PS: " l'image ne passe pas je ne comprends pas pourquoi ^^"
Bonjour
I et J ne sont pas définis. serait-ce les projetés sur les axes ?
moi aussi je pensais que le repère était (O,I,J)
Malheureusement , je ne suis pas chez moi je ne peux pas mettre plus de photos , je sais que j est sur l'axe OJ
Et que AIJ est bien isocèle en A . Avec A et I Sur le cercle et AI = OJ
Merci de vos reponses , en attente d'autres !! 
Plutôt que ce baratin, fait d'affirmations, écris tout le préambule de ton exercice, c'est à dire l'énoncé exact....
encore un(e) qui n'a pas compris qu'on résolvait un exercice avec un énoncé!....
Voici le sujet :
sur le cercle trigonométrique ci contre , le point A est le point asocié au réel pi/5
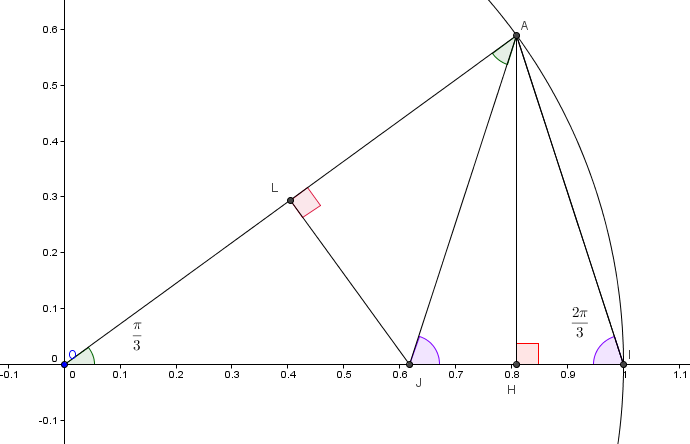
La bissectrice de l'angle OAI coupe le segment [OI] en J
1) démontrer que les triangles OAJ et AJI sont isocèles
2) dans le triangle AIJ , H est le pied de la hauteur issue de A
Démontrer que HI = 1-cospi/5 et en déduire que :
OJ = 2cos pi/5 -1
3) Dans le triangle OAJ , L est le pied de la hauteur issue de J
démontrer que OJ = 1/ 2cospi/5
4)En déduire que (4cos²pi/5)-(2cospi/5)-1=0
Sincèrement désolé j'avais oublié de coter la bissectrice . Aui change tout evidemment 
et je suppose que I est le point de coordonnées (1;0) car le dessin ci contre n'étant pas là, ça aussi faut le deviner!....
sur ton dessin, mets tous les angles que tu connais
dans OAI
O vaut pi/5
somme des angles
d'où A=I=2pi/5 donc isocèle en O
dans AIJ
A=pi/5
or I=2pi/5
somme des angles d'un triangle
donc J=2pi/5
donc isocèle en A
voilà l'idée !
Désolé l'image ne passe pas , j'aurais aimé !
Deja je te remercie pour cette réponse rapide , mais j'aurais juste besoin d'aide pour me débloquer a partir de la question 4 , je ne vois vraiment pas comment raisonner pour avoir des cos carré...
PS: oui , OI=1
PS: oui , OI=1
ce n'est pas du tout ce que j'ai écrit...mais passons....
tu as dit être bloqué à la question 1
je débloque cette question et 7 minutes plus tard tu dis être bloqué à la question 4
soyons sérieux un peu....
Encore un manque de précision de ma part ,
J'etais bloqué question 1 oui , mais entre temps j'ai reussi a trouver le raisonnement avec les pi /5 et 2pi/5 pour prouver AIJ et OAJ grace a votre aide , merci.
Maintenant , je suis bloqué a la question 4 
Vraiment désolé pour mes imprecisions :/
?
Êtes-vous d'accord avec cette égalité : ?
en regroupant
on réduit au même dénominateur et on obtient
Exact , je n'avais pas simplement saisi le therme regrouper ,
Je remercie tous ceux qui m'ont aidé !!