Je suis bloqué à mon dm de maths j'aimerai bien un peu d'aide merci de votre compréhension

Partie A

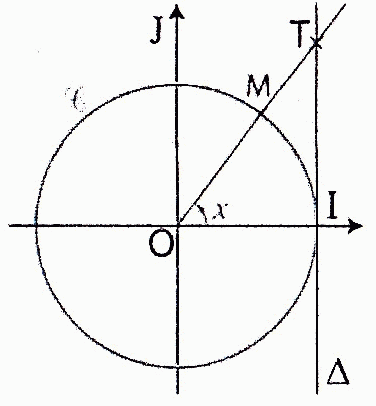
C est le cercle trigonométrique ci contre, delta est la perpendiculaire à (OI) passant par I et M est un point de C tel que (OI;OM)=x
déterminer en fonction de x les coordonnées du point d'intersection T des droites (OM) et delta

Partie B

la fonction tangente est définie pour x différent de pie/2 + kpie ( K appartenant à Z ) par tanx = sinx/cosx
1) on note T la courbe représentative de la fonction tangente dans un repère orthogonal
   Montrer que le point O est un centre de symétrie de T

J'avais pensé à cette méthode : le point O(0;0) et après faire avec f(a+h)+f(a-h)=2b

2)a) déterminer lim tan h quand h tend vers 0

On trouve une forme indéterminé et je ne sais pas comment la résoudre ..

2)b) pour tout nombres réels a et b de ]-pi/2 ; pi/2[ on a tan(a+b)=( tan a + tanb) / (1- tan a tanb)
     Exprimer en fonction de a et h le rapport : tan(a+h)-tan a / h

Pour cette question je n'ai aucune idée ...

c) etudier la derivabilité en 0 de la fonction tangente

faut il faire f(a+h)-f(a) / h avec a tend vers 0

d) en deduire une equation de la tangente t au point d'abscisse 0
   il faut utiliser y=f'(a)(x-a) + f(a) suivant le résultat de la question c

3)a etudier la limite de tan en pi/2 a gauche puis dresser son tableau de variation sur I
     aucune idée ..

je vous remercie par avance de votre aide ..