Inscription / Connexion Nouveau Sujet
DM: exercice sur une fonction rationnelle
Bonjours, j'ai un DM de maths à rendre pour vendredi et j'aurai besoin de votre aide pour quelques points. Je vais vous écrire les réponses que j'ai trouvé( qui peut être sont fausses).
Voici l'énoncé:
Soit f:x--> (-x²+5x-4)/2x et Cf la courbe représentative de f dans un repère orthonormal.
I- Etude Générale de la fonction f:
- ensemble de définition
- limites et asymptotes
- dérivée et variations
- éléments de symétrie
II- Complément à l'étude de f:
a) Déterminer les points d'intersection de Cf avec l'axe (Ox)
b) Exprimer l'équation de la tangente à Cf en A(0;1)
III- Courbes tangentes:
Soit g:x--> mx²+nx+p et Pg la courbe représentative de g dans un repère orthonormal.
a) Exprimer g'(x)
b) Déterminer les paramètres m,n et p (réels) tels que les conditions suivantes soient réunies:
(1) Cf et Pg se coupent en I(-2;9/2)
(2) Cf et Pg ont leur tangente commune en A(1;0)
On sera amené à résoudre un système de 3 équations à 3 inconnues (m,n et p).
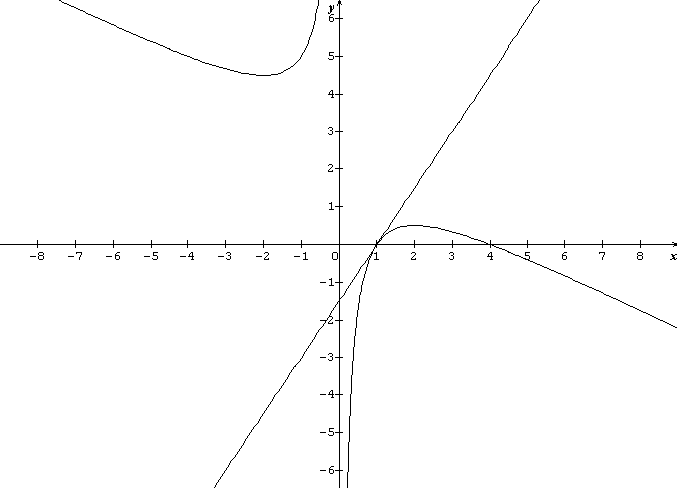
IV- Construire, dans un repère orthonormal du plan d'unité 1cm,
- les courbes Cf et Pg (avec g fonction trouvée au III-b)
- les asymptotes éventuelles à Cf
- les éléments de symétrie éventuels à Cf et Pg
- la tangente commune en A(1;0) à Cf et Pg
V- Démontrer que Cf et Pg n'ont pas d'autres points communs que A et I.
J'ai répondu pour le moment aux deux premieres parties:
I- ensemble de def: R étoile ou ]-00;0[ U ]0;+00[
- dérivée et variations:
f'(x)= (2x²-8)/4x², ensuite j'ai calculé f'(x)=o où j'ai trouvé 2sols: -2 et 2, ensuite, je ne sais pas comment justifié le signe de f' sur les différents intervalles(j'ai pense au théoreme avec le signe de a... mais ici on a une fonction rationnelle donc je sais pas si ça marche) Puis pour continuer, j'énonce le théorème qui dit que lorsque que f' est positive sur un intervalle I, f est croissante.... et j'en viens au tableau de signe de f' et variations de f,le voici:
Signe de f' -00;-2 -> + -2;2 -> - 2;+00 -> +
Mais sur la calculette, je ne trouve pas les bonnes correspondances pour la courbe de f: f décroissante sur -00;-2 puis croissante jusqu'à 0 ou y a la valeur interdite, puis croissante de 0 à 2 et décroissante de 2 à -00.
Je n'arrive pas à voir l'erreur que j'ai faite!
- limites et asymptotes: pas encore fait
- éléments de symétrie: j'ai essayé avec le cours sur la fonction paire ou impaire mais je trouve qu'elle n'est ni impare ni paire ou alors paire mais d'une drôle de façon!
II- Complément à l'étude f:
- points d'intersection avec l'axe Ox équivaut à résoudre f(x)=0 ou je trouve comme solutions: 1 et 4
- equation de tangente: je trouve y= -3/2+3/2x
Voilà ou j'en suis pour le moment, merci d'avoir au moins lu le sujet  .
.
Bonjour,
Il y a effectivement un erreur de signe dans f'(x) ce qui explique la différence dans les variations.
Je trouve
En effet, f n'est ni paire, ni impaire mais sur la courbe, on devine une certaine symétrie, mais pas facile à définir.
Ok pour le II
Pour la dérivée, je part de cette formule: (u'v-uv')/v² avec u= -x²+5x-4 u'=-2x+5 v=2x et v'=2, ah non c'est bon je vois ou je me suis trompé, dans le premier facteur j'ai mis u au lieu de u' je vois l'erreur.
Donc les solutions de l'équation f'(x)=0 sont les mêmes -2 et 2, ensuite il faut que justifie la ligne des signes de f'(x) dans le tableau et je ne sais pas quoi utiliser, dois je utiliser le théoreme avec le signe de A ou alors en résolvant l'inéquation: (-x²+4)/2x² 0, ce qui donne:
0, ce qui donne:
-x²+4 0
0
-x² -4
-4
x² 4
4
deux sols: x -2 et x
-2 et x 2
2
Donc le signe de f'(x) est positive sur l'intervalle [-2;2]
Je pense que l'inéquation est le mieux adapté
Pour ce qui est du tableau de signe et de variations, c'est ok maintenant pour la 1ere partie, il me manque les asymptotes, mais je ne sais pas lesquelles calculer??? en faite je sais pas si faut calculer les 4 c-a-d avec x qui tend vers -00 ou +00 ou 0+ ou 0-.Sinon je sais que pour la limite en l'infini (donc la sa marche pour -00 e +00) d'une fonction rationnelle est = à la limite en l'infini du quotient des termes du plus haut degré.
Apres pour l'asymptote, je pense qu'il n'y en a que deux et qu'elles sont verticales( si la limite en l'infini est finie alors il y a une asymptote verticale) mais apres je ne sais pas le prouver...
Bonjours, c'est encore moi... Le prof nous a laissé le weekend pour finir le dm mais je n'arrive toujours pas à le finir!
Je bloque pour la première partie aux éléments de symétrie ainsi qu'a la 3 eme partie ou je ne sais pas comment faire pour résoudre le systeme à 3 équations, en faite, je trouve pas quelles équations il faut que j'arrive à résoudre, pouvez m'aider svp!!!
Bonjour,
On peut vérifier que f(-x)=-f(x)+5
Ca permet de calculer l'équation de la droite de symétrie.
Pour les asymptotes, il faut écrire f(x) = -x/2 + 5 - 4/x
Quand x est très grand en valeur absolue, le terme 4/x devient très petit. Il reste alors la droite y = -x/2 + 5
Pour la 3ème partie, il faut écrire que I appartient à Pg donc 9/2 = (-2)²m-2n+p
Idem avec l'équation de la tangente en (1;0)
La troisième condition, je n'ai pas encore trouvé. J'y réfléchis.
Bon sang mais c'est bien sûr !
Si les deux courbes partagent une tangente en (1;0), c'est que ce point appartient aussi à Pg donc m+n+p=0
Mais du coup comment on se passe des x dans l'équation de la tangente en 1 ?
3/2x - 3/2 = x(2m+n)-2m+p
Merci beaucoup, je n'y avais même pas pensé !
Vous êtes mon sauveur, godefroy ! J'ai une dette envers vous dorénavant, sachez-le !
Cependant pour la droite de symétrie je ne trouve pas l'équation de la droite de symétrie, voici ce que j'obtiens :
f(-x) = -f(x) + 5
-2x²-10x=0
Je ne vois pas comment en déduire une équation de droite, merci d'avance 
En fait oublies mes deux derniers posts,
alors j'ai calculé d'une part f(-x) et d'une autre part -f(x)+5 et je trouve deux expressions opposés.
Pour en revenir au système, quand on remplace x par 1 on se retrouve avec la même équation que f(1)=g(1)
Je vous en supplie, comment je peux trouver la troisième équation ?
j'ai : 9/2 = 4m+4n+p
0 = m + n + p
et quand je remplace x par 1 dans celle de la tangente je retrouve la seconde équation que j'ai notée.
Bonjours, je suis désolé mais j'en reviens toujours à la premiere partie, comment trouve t'on les éléments de symétrie et comment peut on expliquer le raisonnement qui permet de les trouver.
PS: MW3 tu peux me donner tes résultats pour les limites et les asymptotes pour comparer, Merci.
Le système qu'on doit résoudre est:
4m-2n+p=9/2
m+n+p=0
2m+n=3/2
Mais j'arrive pas à trouver les valeurs des inconnues...
Bonjour,
C'est le bon système.
On peut le faire par élimination ou avec le déterminant.
Je trouve m=1, n=-1/2 et p=-1/2
Ca donne une courbe comme ça
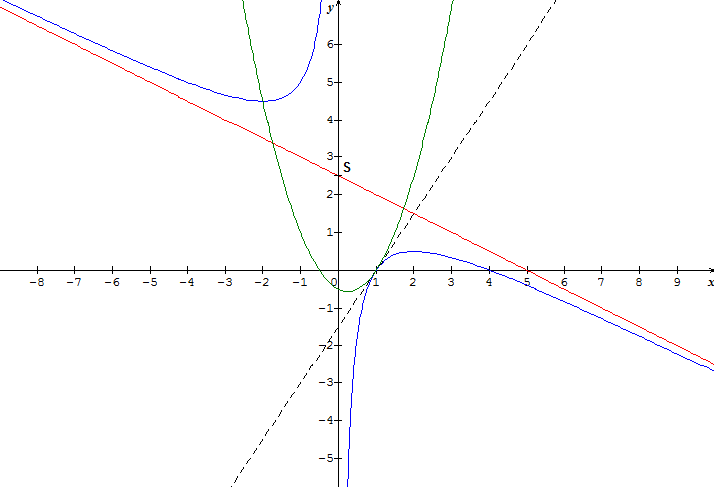
Sinon, pour la symétrie, je ne pense pas qu'on te demande de trouver la droite de symétrie. C'est un peu compliqué.
Je l'ai "intuité" d'après le dessin et ensuite j'ai cherché la différence entre f(-x) et f(x).
A moins que quelqu'un connaisse une méthode simple ???
Je crois que ça te serait plus utile de le trouver toi-même (tu es en terminale quand même). En plus, tu as déjà le résultat.
Avec un peu de rigueur, ce n'est pas très compliqué. 
C'est bon je l'ai trouvé 
Pour démontrer que A et I sont les deux seuls points communs des deux courbes ont résout:
f(x)=g(x)
je trouve sa pour le discriminant:
0=-2x²+11/2x-7/2
mais sa doit pas être ça car par rapport à la courbe ca ne correspond pas
Pour le système il suffisait de prendre :
f(1) = g(1) et f(-2)=g(-2)
On trouve g(x) = 3/2x²-3/2
Cependant pour la dernière équation je bute sur une équation de troisième degré :
6x^3+2x²-16x+8=0
Sauriez vous comment la résoudre ?
Je trouve g(x) = 3/2x²-3/2 et je t'assure que ça marche.
On obtient une parabole qui coupe Cf en A et I.
Cependant à l'exo 5,
je suis bloqué à 6x^3+2x²-16x-8=0
Si tu le dis est ce que tu pourrais me donner tes resultats pour les limites ainsi que les asymptotes pour comparer?
f(x) = g(x) donne 2x3-6x+4 = 0
Comme on sait que A(1;0) appartient aux 2 courbes, x=1 est une des racines de ce polynôme. Donc, on peut le factoriser par (x-1)
Je vous laisse continuer ...
Je trouve g(x) = 3/2x²-3/2 et je t'assure que ça marche.
Non, ça ne marche pas, les 2 courbes n'ont pas la même tangente en A.
Je n'arrive pas à effectuer le développement du système, à chaque fois je trouve des choses aberrantes et je m'embrouille avec toutes ces lettres.
J'essaie d'utiliser la substitution mais rien à faire...
Pitié, ça fait 1 heure que j'essaie tout ce qui est en mon pouvoir pour trouver g(x),
mais je tombe jamais sur vos valeurs, je vous en prie, ce devoir est très important pour moi.
Déjà, ton système doit-être:
4m-2n+p=9/2
m+n+p=0
2m+n=3/2
Ensuite tu isole n:
n=3/2-2m
Donc:
3/2-2m+m+p=0
4m-2(3/2-2m)+p=9/2
Tu fais pareil pour p:
p=-3/2+m
Donc:
4m-2(3/2-2m)-3/2+m=9/2
A partir de là, tu résouds la derniere équation, tu vas trouver la valeur de m et ensuite tu la remplace dans les deux autres équations.
Est ce que tu pourrais me donner les résultats de tes limites et asymptotes stp.


