Inscription / Connexion Nouveau Sujet
DM - Fonctions, carré et triangle 
Bonjour,
Il y a un DM que je dois faire pour la rentrée, j'ai beaucoup de mal :/
Pourriez vous m'aider ?
Merci 
Le motif représenté ci-dessous est décrit ci-après :
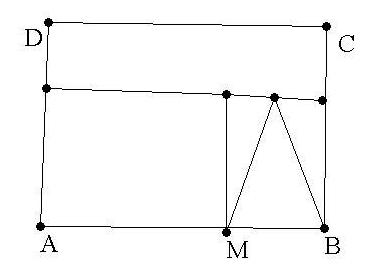
Le carré ABCD a un côté qui mesure 8cm. M est un point du segment [AB]. On dessine comme ci-contre dans le carré ABCD :
. Un carré de côté [AM]
. Un triangle isocèle de base [MB] et dont la hauteur a la même mesure que le côté [AM] du carré.
On s'intéresse aux aires du carré, du triangle, du motif constitué par le carré et le triangle et on se pose les questions suivantes :
1. Quelles dimensions faut-il donner au carré de côté [AM] pour que le motif ait une aire égale à la moitié de celle du carré ABCD?
2. Est-il possible que l'aire du triangle soit égale à laire du carré ?
3. Pour quelle(s) valeur(s) de AM l'aire du triangle est-elle la plus grande ?
4. Est-il possible de faire en sorte que l'aire du triangle soit plus grande que celle du carré ? Si oui, préciser pour quelle(s) valeur(s) de AM c'est possible.
5. Comment évolue l'aire du motif en fonction de AM ? En fonction de MB ?
Merci d'avance, je suis vraiment perdu.. :/
Bonsoir,
Pourquoi perdu ? ça ne demande que des connaissances élémentaires. Pose x=AM
l'aire du motif c'est l'aire du carré plus l'aire du triangle. Que vaut l'aire du carré en fonction de x ?
Que vaut l'aire du triangle ? que vaut la somme des deux ? Que vaut l'aire de ABCD ?
Ecrit l'équation qui signifie que l'aire du motif est égal à la moitié de celle de ABCD.
Aire du carré vaut : AM² soit x² ?
Aire du triangle vaut : (MB * MG)/2 = x(8-x) donc 8x -x²
La somme des deux, donc le motif, vaut 8x-x² + x² = 8x ?
Et l'aire de ABCD vaut 8² = 64 ?
En fait, ce qui me bloquait c'était de poser la problématique : soit AM = x
Ecrire l'équation qui signifie que l'aire du motif est égal à la moitié de celle de ABCD.
Il faut résoudre : 8x = 1/2(64) ?
Donc 8x = 32
x = 32/8
x = 4
L'aire du motif est égal a la moitié de l'aire de ABCD pour x = 4 ?
D'accord
Donc pour 2, si j'ai bien compris :
Il faut résoudre x² = 8x-x²
x² + x² = 8x
2x² = 8x
2x² -8x = 0
x(2x-8) = 0
Un produit de facteur est nul si et seulement si au moins 1 de ses facteurs est nul.
x = 0 ou 2x-8 = 0
x = 0 ou 2x = 8
x = 0 ou x = 4
Il est possible que l'aire du triangle soit égale à l'aire du carrée pour AM = 4 ?
non, nous avons fait une erreur. l'aire du triangle c'est base x hauteur / 2, tu as oublié de diviser par 2, c'est MB.AF/2 donc x(8-x)/2
il faut refaire la question 1
Ah :/
Donc x(8-x) / 2 = 8x -x² / 2 = 4x - (1/2)x²
La somme des 2 motifs vaut x² + 4x - (1/2)x²
La somme des deux motifs vaut (3/2)x² + 4x
(3/2)x² + 4x = 1/2(64)
(3/2)x² + 4x - 32 = 0
... Je peux rien faire !
oui une équation du second degré, écrit là x²+8x-64=0
tu n'as dû encore apprendre le discriminant ? et la forme canonique ?
Ah oui, dans mon DM il est dit qu'après, nous ferons une lecture graphique
Je complèterais donc plus tard !
2. Est-il possible que l'aire du triangle soit égale à l'aire du carré ?
x² = 4x - 1/2 x²
x² - 4x + 1/2x² = 0
3/2 x² - 4x = 0
x(3/2x - 4) = 0
x = 0 ou 3/2x = 4
x = 0 ou x = 8/3
oui c'est ça (et on peut remarquer que pour x=0 les deux figures sont aplaties et leur aire est nulle pour les deux)
3. Pour quelle(s) valeur(s) de AM l'aire du triangle est-elle la plus grande ?
Là par contre, j'ai totalement AUCUNE idée :/
(tout comme les autres questions..)
Donc :
? (A partir de cette ligne cela me semble faux !)
x > 0 ou -3x + 8 > 0
x > 0 ou -3x > -8
x > 0 ou x < 8/3
L'aire du triangle est la plus grande pour
non, tu veux le signe de -3x²+8x, c'est un polynôme du second degré. Il est du signe de a donc négatif ici quand x est à l'extérieur des racines qui sont 0 et 8/3, donc il est positif entre 0 et 8/3
Ah d'accord :/
Mais peut-on émettre des hypothèses là-dessus ?
4. Est-il possible de faire en sorte que l'aire du triangle soit plus grande que celle du carré ? Si oui, préciser pour quelle(s) valeur(s) de AM c'est possible.
5. Comment évolue l'aire du motif en fonction de AM ? En fonction de MB ?
Et bien résout les équations correspondantes. Si tu as compris ce qui précède, ça ne devrait pas te poser de problème.
3. Pour quelle(s) valeur(s) de AM l'aire du triangle est-elle la plus grande ?
donc le maximum de la fonction x(8-x)/2 ? C'est une parabole tournée vers le bas. Son maximum est pour -b/2a ou bien la demi somme des racines donc x=4 (M au milieu de AB)
Bonjour, j'ai le même dm pour la rentrée mais je n'ai que t'a question 2 " est-ce possible que l'aire du triangle soit égal a l'aire du carré ? " Et je me demande comment faire pour montré car j'ai fais les calcules mais je me demande si je dois faire un graphique a l'aide de ma calculatrice pour voir si à un moment les deux droites se croisent, voilà merci ^^'
Si tu as fait les calculs et répondu à la question, tu n'as pas besoin de faire de graphique ni d'utiliser ta calculatrice.
Si tu as fait les calculs et répondu à la question, tu n'as pas besoin de faire de graphique ni d'utiliser ta calculatrice.
Bas j'ai essayé de faire l'inequation
x^2 = 4x-(1/2)x^2 mais je n'y arrive pas et d'après ce que je me rappelle ma prof nous a parlé de polynôme du second degré.
D'accord, après j'avais vue votre réponse au dessus mais je ne comprend pas le
x^2-4x+ (1/2x^2)=0
(3/2x^2)-4x=0
x(3/2x-4)=0
x²+x²/2 ça se regroupe
ça donne 3x²/2 -4x = 0, on mets x en facteur
x(3x/2-4) = 0 et on annule chaque facteur
on trouve x=0 donc M en A et toutes les aires sont nulles
et puis l'autre solution 3x/2 = 4 donne x = 8/3
Annuler
connectez vous