Bonjour,

j'ai un DM a rendre pour la rentré et j'aimerai qu'on me corrige si il y a besoin.

Enoncé :

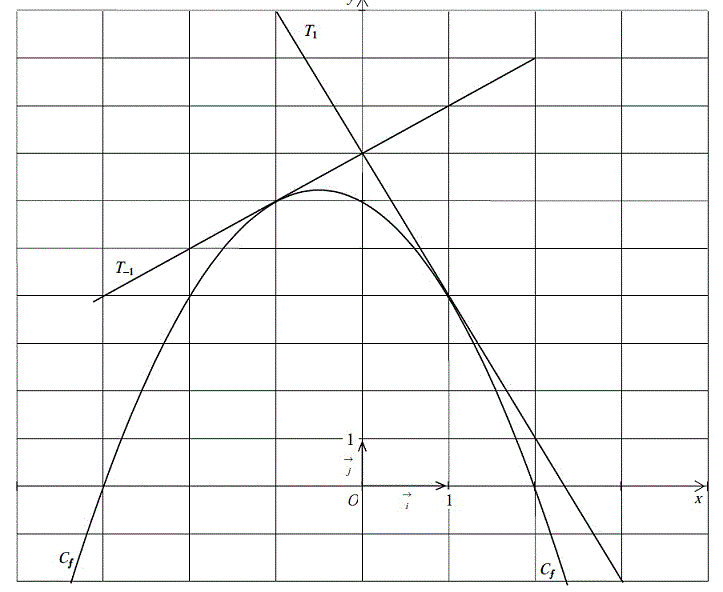
On dispose d'une courbe C¦ représentant une fonction ¦ et de deux de ses tangentes T1 et T-1.
(Voir graphique ci-contre) *** (lien supprimé) ***
On sait que la fonction ¦ est de la forme : ¦(x) = a x2 + bx + c. (C¦ est une parabole)

1. Par lecture graphique, donner la valeur de ¦(0). En déduire la valeur de c.

2. Exprimer ¦'(x) en fonction de a et b.

3. Par lecture graphique, donner la valeur des nombres ¦'(1) et ¦'(-1). En déduire la valeur de a et b.

4. Par lecture graphique, résoudre l'équation ¦(x) = 0. Retrouver ce résultat par calcul.


Réponses :

1. f(0) = 6 Sachant que f(0) = c ; c = 6

2. f'(x) = 2ax + b

3. f'(1) est le coefficient directeur de la tangente T1.
   Par lecture graphique, on trouve f'(1) = -3

   f'(-1) est le coefficient directeur de la tangente T-1.
   Par lecture graphique, on trouve f(-1) = 1

La question 2 nous a permis de voir que f'(x) = 2ax + b donc :
f'(1) = 2a + b    ;    f'(-1) = -2a + b

On va donc résoudre le système suivant : ( 2a + b = -3
                                                             ( -2a + b = 1

Pour cela, on va utiliser les matrices ;

on nomme A la matrice (2 1)
                                (-2 1)

               B la matrice (-3)
                                ( 1)

               X la matrice (a)
                                (b)

AX = B
A^-1B = X

Par la calculatrice on trouve X = {( -1 ; -1 )}
Donc a = -1 et b = -1

Sachant que la fonction f est de la forme ax² + bx + c, la fonction f: f(x)=(-1)x² + (-1)x + 6 soit -x² -x + 6

4. L'équation f(x) = 0 peut se résoudre graphiquement, en effet les solutions de cet équation correspondent aux points d'intersection de Cf avec l'axe (Ox) sur l'axe des abscisses.
On trouve donc X1 = -3 et X2 = 2
S = {-3;2}

Par le calcul :

On va résoudre l'équation f(x) = 0 soit -x² -x +6 = 0
Delta = b² - 4ac
Delta = (-1)² - 4 x -1 x 6
Delta = 25

Delta > 0 donc 2 solutions :

X1 = -3   et X2 = 2

On retrouve X1 = -3 et X2 = 2
S = {-3;2}