Inscription / Connexion Nouveau Sujet
dm intégrale,aire sous la courbe...
bonjour, j'ai un dm à faire et je galère
on est dans u plan orthonormal o i j
et f est définie sur [0, pi] et C est sa représentation graphique et D est l'ensemble des points M(x,y) tels que 0≤ x ≤ pi et
0≤ y ≤ f(x)
1) tracer C sans justification et hachurer D
2) calculer en cm^2 l'aire du domaine D, on rappelle que sin^2x=(1/-cos2x)/2
1)
ah zut, ça bug ,j'essaie de mettre la 1) et tout n'est pas passé
et f(x)=sin^2 x , c'est vrai que sans c'est pas possible 
3) montrer que sin^4x =(1/8)(cos4x)-(1/2)cos2x+ (3/8)
on pourra utiliser les formules d'Euler et en déduire la valeur de I= (intégrale) de 0 à pi de sin^4x dx
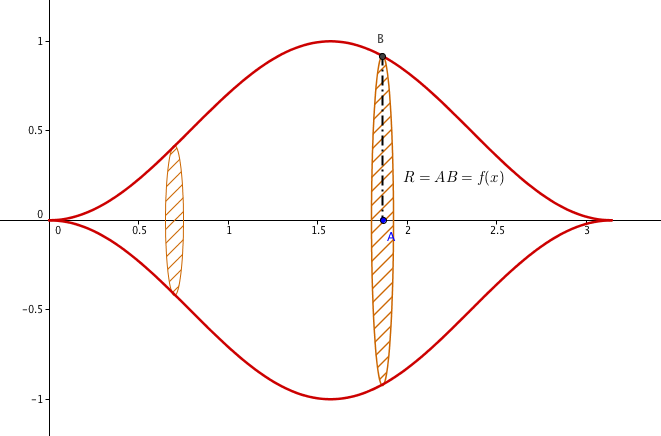
4) A est un point de l'axe des abscisses , d'abscisse x appartient [0, pi ] et B est le point de C de même abscisse. Le segment [AB] pivotant autour de l'axe (O, i) engendre un disque de l'espace. Exprimer en fonction de x l'aire S(x) de ce disque
5)en déduire le volume en cm^3 du solide de l'espace obtenu par rotation de la courbe C autour de l'axe des abscisses.
si on ne voit pas l'image --> http://hpics.li/86e9406
merci, c'est bien ce que j'ai trouvé =)
pour la 2) je pense qu'il faut calculer l'intégrale de f(x) de 0 à pi
puisque f(x)= (1/-cos2x)/2 alors I=(int 0à pi) 1/-cos2x/2(x)dx
on pose u=-1/2 et u'(x)=-1/2x et v(x)=cos2x et v'(x)=sin2x
c'est bon? souvent je me trompe à ce niveau =)
3)pour Euler, j'ai trouvé (sin^4x=cos4x+isin4x-cos4x+isin4x)/2i mais cela ne me permet pas de trouver le résultat attendu...
Commence par l'avant dernière avant de passer à la dernière.
As-tu compris la question pour commencer ?
oui, on a x sur l'axe des abscisse et B sur C, ces 2 points forment un segment qui tourne autour de O, i formant un disque
je pense qu'il faudrait avoir le rayon selon les positions des points A et B
euhh....je vois le truc mais j'ai du mal a expliquer mais le rayon est nécessaire pour calculer l'aire
Non, tu obtiens le volume du solide de l'espace obtenu par rotation de la courbe C autour de l'axe des abscisses
à ma question 3. avec euler, il fallait montrer que sin^4x= (1/8)(cos4x)-(1/2)cos2x+ (3/8) et en déduire (intégrale de 0 à pi) de sin^4 d(x)
je ne l'ai pas faite donc j'utilise ce résultat en l'intégrant pour trouver ensuite la valeur de mon volume?
celle ci je l'ai faite désolée, ais je ne vois pas comment en déduire k=la valeur de l'intégrale de 0à pi de sin^4x dx





 de 0 à
de 0 à  de 2
de 2

