Inscription / Connexion Nouveau Sujet
DM MATH Convexité et continuité
Bonjours , je dois faire ce Devoir Maison et j'ai du mal , ainsi que tout ce que j'ai fait je ne sais pas si c'est bon
énoncer:
Le directeur d'un parc de loisirs a créé un logo pour son site web symbolisant une rampe de lancement. Pour cela, il a construit dans un repère orthonormé d'unité graphique 1cm, la courbe représentative C de la fonction f définie sur [0;5] par: f(x)= 0,125x3- 0,75x2+ 4
1.a. Déterminer f'(x) (je l'ai déjà fait)
1.b. Remontrer que cette courbe C admet en deux point une tangente horizontale.
1.c. Démontrer que le signe de f'(x)est le même que le signe de x-4 sur [0;5]
2. Déterminer le sens de variation de la fonction f sur [0;5]
3.a. Démontrer que la courbe C admet un point d'inflexion et préciser les coordonnées de ce point d'inflexion
3.b. Déterminer une équation de la tangente T a la courbe C en ce point
Pour la 1 a j'ai trouvée 0.375x²-1.5x
pour la b j'ai cherché le discriminant et trouvé 2.25 puis j'ai cherché x1 et x2 qui est égal à x1= -4 et x2= 0
pour la c je ne sais vraiment pas ce qu'il faut faire
pour la 2 j'ai trouvé
x : 0 -4 0 5
f'(x): + 0 - 0 +
f(x) décroissant puis croissant et enfin décroissant
où 0 = 4 / -4= -16
0 égal 4 / 5= 0.875
pour le 3.a j'ai trouvée un point d'inflexion en -1.5 car j'ai fait f""(x)=0 donc j'ai remplacé les x par 0 .
Je ne sais pas si c'est juste ni comment faire pour la suite, merci.
Bonjour,
1)a) BON
b) Il faut résoudre f '(x)=0
Donc résoudre : 0.375x²-1.5x=0
Pas besoin de discriminant. Cela donne :
x(0.375x-1.5)=0
2 solutions :
x=0 ou 0.375x-1.5=0
x=0 ou x=1.5/0.375=4
Pense à vérifier si une mise en facteurs est possible.
On a donc une tgte horizontale en x=0 et x=4.
c)
On a vu que f '(x)=0 a 2 racines : x=0 et x=4.
On peut donc l'écrire sous la forme :
f '(x)=ax(x-4)
On développe :
f '(x)=ax²-4ax²
On compare avec f '(x)= 0.375x²-1.5x
Ce qui donne a=0.375 et -4a=-1.5 soit a=-1.5/-4=0.375 évidemment.
Donc :
f '(x)=0.375x(x-4)
Sur [0;5] , le facteur 0.375x est positif donc f ' (x) est du signe de son second facteur (x-4). OK ?
2)
f '(x) est du signe de (x-4).
x-4 > 0donne : x > 4.
Donc sur [0;4] , f '(x) < 0
Et sur [4;5] , f '(x) > 0.
x------>0................4....................5
f '(x)->.........-.......0..........+.........
f(x)--->4.........D......0..........C........0.875
D=flèche qui descend
C=flèche qui monte
J'ai calculé f(0) , f(4) et f(5) pour mettre dans le tableau. Tu feras de même.OK?
3)
a)
f " (x)=0.75x-1.5
0.75x-1.5 > 0 donne : x > 2
Donc sur [0;2] , f "(x) < 0
Et sur [2;5], f " (x) > 0.
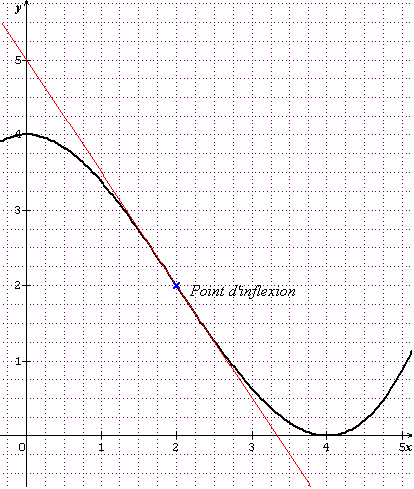
La dérivée seconde s'annule en changeant de signe pour x=2. Donc la courbe admet un point d'inflexion en x=2 qui donne f(2)=2.
Coordonnées du point d'inflexion : (2;2)
3.b. Déterminer une équation de la tangente T a la courbe C en ce point
L'équation d'une tgte à une courbe représentative de la fonction f(x) en un point d'abscisse « a » est donné par :
y=f ' (a) (x-a)+f(a)
Ici a=2
Tu calcules f'(2) et f(2) puis tu arranges.
A la fin , tu auras :
y=-1.5x+5
Je te joins un graph avec la courbe C en noir , la tgte au point d'inflexion en rouge.
Ah et bien merci , les explications sont clairs et précise ! C'est très gentil ! et bien bonne après midi , à bientôt
Bonjour, j'ai ce même exercice à traiter et je n'ai pas compris comment faire pour trouver les 2 solutions.
En effet, après avoir trouvé la dérivée dans le 1) j'ai voulu résoudre f'(x)=0 ce qui donne 0.375x²-1.5x=0
J'ai ensuite fait une factorisation -->
<=> 0.375x*x-1.5x=0
<=> x(0.375x-1.5)=0
Ensuite j'ai voulu passer les termes "de l'autre côté" pour isoler x:
<=> x=1.5/0.375
<=> x=4
Mais je ne comprends pas où va ce x
2 solutions :
x=0 ou 0.375x-1.5=0
x=0 ou x=1.5/0.375=4
De plus, je ne comprends pas non plus pourquoi x=0 ou 0.375x-1.5=0
et x=0 ou x=1.5/0.375=4
Faut-il faire 2 calculs différents pour trouver ces résultats?
Merci, j'espère avoir été assez précise,
A bientôt.
Bonjour madyo,
Ok avec toi jusqu'à : x(0.375x-1.5)=0
Et là, il n'est pas question d'isoler "x" comme tu dis , ce qui est impossible dans une équation du second degré car :
x(0.375x-1.5)=0 est une équation du second degré !!
Tu appliques ( vu en 3ème) :
Un produit de facteurs est nul si l'un au moins des facteurs est nul.
Tu as 2 facteurs donc 2 équations du 1er degré à résoudre.
Donc : x(0.375x-1.5)=0 donne :
x=0 OU 0.375x-1.5=0 --->et pour la 2ème tu isoles "x" car c'est une équation du 1er degré.
x=0 OU 0.375x=1.5
x=0 OU x=1.5/0.375=4
S=[0;4]
OK ? C'est clair ? Non ?
N'oublie pas :
Un produit de facteurs est nul si l'un au moins des facteurs est nul.
Cela te servira plein d'autres fois.
On a vu que f '(x)=0 a 2 racines : x=0 et x=4.
On peut donc l'écrire sous la forme :
f '(x)=ax(x-4)
On développe :
f '(x)=ax²-4ax²
On compare avec f '(x)= 0.375x²-1.5x
Ce qui donne a=0.375 et -4a=-1.5 soit a=-1.5/-4=0.375 évidemment.
Donc :
f '(x)=0.375x(x-4)
Désolé, j'ai encore une question à propos du développement effectué ci-dessus:
En essayant de développer j'ai trouvé f'(x)=ax²-4ax donc je me demandais comment vous aviez fait pour trouver "-4ax²"
Pardon, je n'avais pas fini mon message:
Pourquoi doit on écrire sous cette forme: f'(x)=ax(x-4) si ensuite on reprend le premier résultat de la dérivée pour le comparer?
J'essaie vraiment de comprendre ce que je dois faire et je vous prie de m'excuser pour toutes ces questions
Merci, à bientôt.
Bonjour madyo,
En essayant de développer j'ai trouvé f'(x)=ax²-4ax donc je me demandais comment vous aviez fait pour trouver "-4ax²"
Comme tu t'en doutes , c'est une faute de frappe !! Tu sais , je ne me relis pas toujours, hélas!
Bien sûr : f '(x)=ax(x-4) donne f '(x)=ax²-4ax.
Pourquoi doit on écrire sous cette forme: f'(x)=ax(x-4) si ensuite on reprend le premier résultat de la dérivée pour le comparer?
Tu as raison mais alors il faut trouver un autre raisonnement que le mien pour répondre à la 1) c) qui est :
1.c. Démontrer que le signe de f'(x)est le même que le signe de x-4 sur [0;5]
f (x)=0.125x3-0.75x2+4 , ce qui donne :
f '(x)=0.375x2-1.5x
Je te laisse trouver une démonstration pour montrer que ce f '(x) est du signe de (x-4). Tu peux l'envoyer que je la voie si tu as des doutes.
hello, jai le même exercice seulement a la fin l'on me demande: Que peut on dire de la position relative de T et de Cf
merci davance
Bonjour
Donner la position relative des deux courbes c'est dire laquelle est au-dessus de l'autre
Pour ce faire, on étudie le signe de la différence
On considère un point M appartenant à la courbe représentative de . Il a donc pour
coordonnées .
On considère maintenant un point N de même abscisse que M, appartenant à la courbe représentative de .
Ici sera la fonction affine dont la courbe représentative est T. Le point N a donc pour coordonnées
Pour étudier la position relative des deux courbes on veut savoir si l'ordonnée de M est plus grande que l'ordonnée de N ou le contraire.
est équivalent à
ou encore
On étudie donc le signe de la différence
si alors
par conséquent la courbe représentative de
est au-dessus de la courbe représentative de
si alors
par conséquent la courbe représentative de
est au dessous de la courbe représentative de
si alors on a un point d'intersection des deux courbes




