- Bissectrice et cercle inscrit dans un triangle - Cours 4ème
- Exercice Bissectrices et cercles inscrits dans un triangle
- Cours sur les Figures planes, Distance d'un point à une droite et Tangente à un cercle
- QCM : Figures planes, distance et tangente - Exercice 4ème
- Six Exercices de géométrie pure - quatrième
Inscription / Connexion Nouveau Sujet
DM n°10
Bonjour,
J'aurai besoin d'aide pour mon DM dont voici l'énoncé:
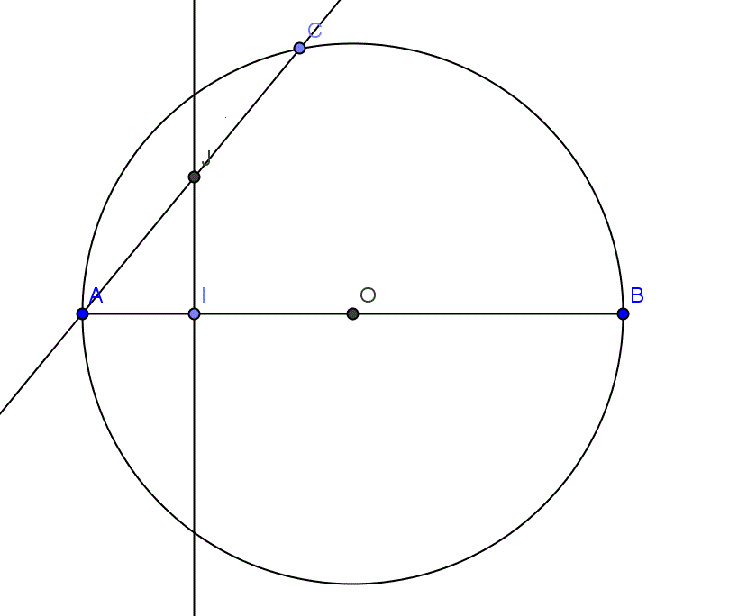
[AB] est un segment. On appelle C le cercle de diamètre [AB].
C est un point de C distinct de A et B.
I est un point sur le segment [AO]. (O étant le centre du cercle).
La perpendiculaire à (AB) passant par I coupe (AC)en J.
1) Montrer que le triangle ABC est rectangle en C.
2) Montrer que les points I,B,C et J sont cocycliques.
3)Tracer ce cercle puis expliquer sa construction.
Je suis novice sur ce site et nulle en maths et je ne sais pas comment on fait pour tracer la figure avec l'ordi.
Voici ce que j'ai commencé à faire :
Sur ma feuille, j'ai tracé le segment [AB] j'ai pris le milieu O et j'ai tracé le cercle de centre O et de rayon AO puis j'ai placé le point I sur le segment [AO] et j'ai tracé une perpendiculaire à (AB). Je trouve que I est un angle droit mais je ne sais pas continuer pour placer C et donc J. Si je n'arrive pas à placer C je ne peut pas répondre à la première question.
Merci de venir à mon secours et si possible de me faire voir la figure
Bonjour,
C est un point quelconque du cercle, tu peux donc le prendre ou tu veux sur le cercle (à l'exception de A et B)...
merci Tilk11 et natylilou mais j'aurai besoin d'une précision pour répondre à la question 1. Si je relie BC, je vois bien que le triangle ABC est rectangle en C mais à l'oeil et avec mon équerre mais je ne sais pas l'expliquer mathématiquement.
Pour la question 2 et 3, j'ai tracé le cercle IBCJ en prenant comme milieu pour la pointe de mon compas le milieu de BJ comme ça, les 4 points sont sur le cercle donc cocycliques mais je ne sais pas expliquer la construction de ce cercle et je ne sais pas si mon explication pour cocycliques est suffisante.
On a pas encore fait la leçon et je devais chercher sur internet cocyclique et j'ai trouvé que c'était des points non alignés mais qui appartenaient à un même cercle. mais en exemple ça disait aussi que 4 points non alignés sont cocycliques si et seulement si (CA,CB)=(DA,DB). Il y avait des flèches sur CA CB DA DB mais je ne sais pas les faire avec mon clavier et il y avait une figure d'un cercle et les 4 points dessus (j'ai trouvé ça sur bibmath.net)
Vous seriez super sympa de m'expliquer la construction du cercle IBCJ et pourquoi IBCJ sont cocycliques.
merci beaucoup
pour démontrer que ABC est rectangle en C, pense au théorème suivant, tu le connais peut-être sous une autre forme...
"Si, dans un cercle, un triangle a pour sommets les extrémités d'un diamètre et un point de ce cercle, alors le triangle est rectangle en ce point"
pour la question suivante, tu peux utiliser le théorème suivant, tu le connais peutêtre sous une autre forme :
"Le cercle circonscrit à un triangle rectangle a pour diamètre l'hypoténuse et son centre est le milieu de l'hypoténuse"
Bonjour,
Merci Tilk_11, mais pour la question 3, si j'applique le théorème direct qui dit que " Si un triangle est rectangle alors son hypoténuse est un diamètre de son cercle circonscrit " et que dans un triangle rectangle le milieu de l'hypoténuse est le centre du cercle circonscrit au triangle et la longueur du segment qui joint le sommet de l'angle droit au milieu de l'hypoténuse est la moitié de la longueur de l'hypoténuse.
où le théorème réciproque " si l'un des côtés d'un triangle est un diamètre de son cercle circonscrit alors ce triangle est rectangle"
Ces 2 théorèmes répondent à la question 1 pour prouver que le triangle ABC est rectangle en C mais ça ne m'aide pas pour expliquer la question 3 : Comment j'ai construit le cercle IBCJ car pour faire ce cercle, j'ai mis la pointe du compas sur le milieu du segment BJ que j'ai tracé mais comment expliquer comment j'ai trouvé ce point
merci de m'aiclairer
bonjour,
en utilisant les propriétés précédentes :
le triangle BIJ est rectangle en I par construction, donc le centre de son cercle circonscrit est le milieu de son hypoténuse soit le milieu de [BJ].
de plus ABC est un triangle rectangle d'après le 1). donc BJC est aussi un triangle rectangle, les points A, J et C sont alignés. le cerce circonscrit à BJC a lui aussi pour centre le milieu de [BJ]. 'est le même cercle, les points B, J et C sont cocycliques et la construction est justifiée..
Bonjour et merci natylilou
Je voudrai confirmation sur les réponses que j'ai mis dans mon DM et si j'ai oublié quelque chose ou mis quelque chose de faux peux-tu me les corriger s'il te plait.
Pour la question 1: j'ai mis que j'utilisai le théorème réciproque :" Si l'un des côtés d'un triangle est un diamètre de son cercle circonscrit alors ce triangle est rectangle" (le diamètre du cercle circonscrit est alors son hypoténuse).
ABC sont des points sur le cercle de diamètre [AB]
O est le milieu du côté [AB] du triangle ABC
CO=1/2AB alors le triangle est rectangle en C
Pour la question 2 : J'ai mis que j'utilise le théorème direct :"si un triangle est rectangle alors son hypoténuse est un diamètre de son cercle circonscrit"
Comme ABC est un triangle rectangle en C,JBC est un triangle rectangle en C car les points AJC sont alignés.
Le cercle de diamètre [JB] passe par C
M est le milieu de [JB]
MC=MJ=MB=1/2JB
Les points IBCJ sont cocycliques car ils sont sur le même cercle.
Pour la question 3 :
J'ai mis que pour obtenir le centre du cercle circonscrit, il suffit de tracer les médiatrices de deux côtés.
La médiatrice de [CJ], [BC] et [IB] se coupe en un même point M qui est le centre du cercle circonscrit.
Le cercle de diamètre JB passe par les points CJIB
merci de me dire si je peux recopier mon DM tel que.
Bonjour,
pour la question 1 on te demande de démontrer que le triangle ABC est rectangle....
Pour la question 1: j'ai mis que j'utilisai le théorème réciproque :" Si l'un des côtés d'un triangle est un diamètre de son cercle circonscrit alors ce triangle est rectangle" (le diamètre du cercle circonscrit est alors son hypoténuse).....
le point C étant sur le cercle de diamètre [AB], le triangle ABC est donc rectangle en C
Pour la question 2 : J'ai mis que j'utilise le théorème direct :"si un triangle est rectangle alors son hypoténuse est un diamètre de son cercle circonscrit"
Comme ABC est un triangle rectangle en C,JBC est un triangle rectangle en C car les points AJC sont alignés.
Le cercle de diamètre [JB] passe par C
de même, le triangle IJB étant rectangle en J, le cercle de diamètre [JB] passe par I
Les points IBCJ sont donc cocycliques car ils sont sur le même cercle.
Pour la question 3 :
ce que tu as écrit est parfaitement inutile,
les triangles JCB et JIB sont rectangles et ont la même hypoténuse donc ils ont le même cercle circonscrit dont le centre est le milieu de [JB], l'hypoténuse.
Merci Tilk_11 j'ai juste à te demander une précision : lorsque tu mets pour la question 2 en rouge que le triangle IJB est rectangle en J, es-ce une erreur de frappe ? car il est rectangle en I et non en J
Si je t'ai bien comprise, pour la question 1 et 2 je dois juste mettre les théorèmes et la phrase en rouge que tu as mis en réponse toute mon explication est inutile ou fausse?
Pour la question 3 tu mets que c'est inutile mais es-ce que c'est faux ? car le prof aime qu'on détaille étape par étape la façon dont on s'y est pris pour construire le cercle
merci
oui, c'est une faute de frappe, il est effectivement rectangle en I puisque [IJ] est son hypoténuse...
pour la question 1 : oui
pour la question 2 :
n'oublie pas la partie que tu as écrite et qui suit le théorème...
pour la question 2 :
non ce n'est pas faux, mais pour un triangle rectangle, tu dois savoir que le centre de son cercle circonscrit est le milieu de l'hypoténuse, il n'est donc pas utile de rappeler que le centre du cercle circonscrit se trouve en traçant les médiatrice de plus, dans ce que tu as écrit tu ne précises pas où est exactement ce point M ....dire que M est le milieu de [JB] est précis et te permet de faire une construction simple de ce centre....