J'ai un DM à faire pour vendredi mais je n'ai pas compris quelques question ou du moins je ne sais comment y répondre. J'ai préciser que j'ai déjà fait certaines questions  Voici l'énoncé complet et les questions :

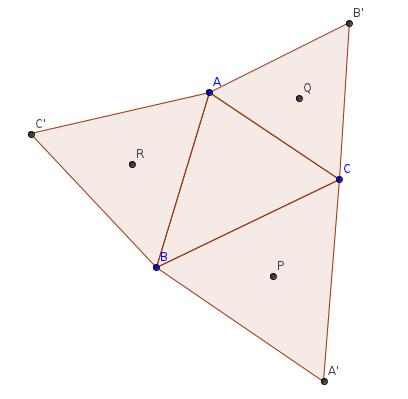
Dans un le plan orienté muni d'un repère orthonormal direct, on considère ABC  un triangle direct sur lequel on construit extérieurement trois triangles équilatéraux BCA', ACB', et ABC'.
On considère les points P, Q et R centres de gravité respectifs des triangles BCA', ACB' et ABC'
On note a,b,c,a',b',c',q,p,r les affixes respectives des points A,B,C,A',B',C',P,Q,R.
P, Q, et R centre de gravité des triangles BCA', ACB' et ABC'.

1)a) Traduire avec les affixes concernées, que C' est l'image de A dans une rotation d'angle de mesure /3 dont on précisera le centre (déjà fait)
b) Montrer que a'+b'+c'= a+b+c (déjà fait)

2) En déduire que p+q+r=a+b+c (pas fait)
3) En déduire que les triangles ABC, A'B'C' et PQR ont même centre de gravité (pas fait
4) Montrer que : 3(q-p)= (b'-c)+(c-a')+(a-b) (pas fait)
   Montrer que : 3(r-p)= (a-c)+(b-a')+(c'-b) (pas fait)

5) Justifier les égalités suivantes : (déjà fait)
a) a-c = e^(i/3)*(b'-c)
b) b-a' = e^(i/3)*(c-a')
c) c'-b = e^(i/3)*(a-b)

6) Déduire des questions 4) et 5) que les triangle PQR est équilatéral

Voila merci de votre aide
P.S : Pas la peine de me répondre pour les questions où il est préciser " déjà fait "