Inscription / Connexion Nouveau Sujet
dm nombres complexes module de z +z'
bonjour,
J'ai un dm sur les complexes à faire pour lundi et je bloque sur la dernière question de cet exercice. J'espère que vous pourrez m'aider. Merci
Soit M(z) et M'(z')
1) Construire le point M'' d'affixe z+z'
2)Reconnaitre le vecteur d'affixe z'-z
3)Donner une condition nécessaire et suffisante sur les points M et M' pour que :
module de z+z'=module de z'-z
j'ai fait la 1 et la 2 mais je bloque totalement sur la 3.
Merci de votre aide 
bonjour merci de m'aider,
les diagonales d'un parallélogramme sont égales lorsque le parallélogramme est un rectangle mais je ne comprends pas pourquoi cela revient à ça ?
les diagonales d'un parallélogramme sont égales lorsque le parallélogramme est un rectangle
Oui, je vais te faire un dessin; sois un peu patient...

Donc voici:
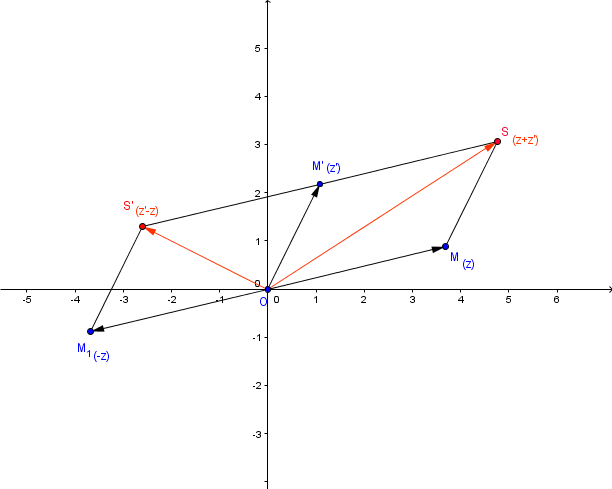
Les parallélogrammes et
sont égaux et
est un rectangle.
Autrement dit le triangle est rectangle en

Merci beaucoup ! 
Donc le point M est sur l'axe des abscisses et M' sur l'axe des ordonnées .
La figure m'a beaucoup plus aidée que la mienne 
Bonne soirée et à bientôt sur l'île 
Donc le point M est sur l'axe des abscisses et M' sur l'axe des ordonnées .
Non,non! Si
La condition nécessaire et suffisante est

euh.. Bah j'ai encore été trop vite ! Je ne pensais plus que M était quelconque...
Merci de m'avoir rectifié!
Bonne soirée et merci de m'avoir aidé 


