Bonjour, Bonsoir !
Il y a un exercice dans un DM sur lequel je bloque.. C'est pourquoi je suis venue vous demander votre aide

Voici l'énnoncé :

"Les mathématiciens grecs représentaient certains nombres entiers naturels géométriquement, comme ici les 4 premiers nombres dits triangulaires."

1. Dessiner les nombres T(5) et T(6)
-> Voir l'image des figures en dessous
Je crois avoir réussi pour cette question, pouvez-vous me dire si elle est correcte ?

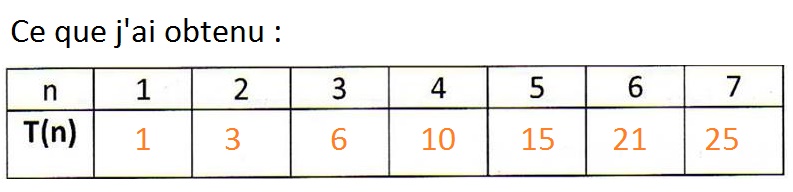
2. Compléter le tableau suivant
-> Voir l'image du tableau en dessous
Pareil que pour la question 1, est-ce juste ?

Je bloque pour ces questions :
3. On veut maintenant déterminer la forme algébrique du nombre T(n) en fonction de n. Pour cela, on assemble 2 nombres T(n) comme ci-contre pour former un rectangle. Déterminer T(n) en fonction de n.
Aide: Penser à l'aire du R....

4. Calculer les 12ème et 100ème nombres triangulaires T(12) et T(100) à l'aide de cette formule.  

5. Existent-ils des nombres triangulaires valant : 1er cas : 378 ; 2eme cas : 2 671
   Si la réponse est oui, donner le rang n associé à T(n) sinon donner la valeur du nombre triangulaire le plus proche                   et son rang n.
Aide : vous utiliserez le menu TABLE de la calculatrice en saisissant Y1 = .... puis en sélectionnant dans RANG ou SET (Casio) 0 en valeur initiale ; 100 en valeur finale sur Casio uniquement avec un pas de 1.

Voilà les images, dans l'ordre :