Inscription / Connexion Nouveau Sujet
DM prouver une limite d'une exponentielle
Bonsoir,
voilà je viens de commencer le cours sur les exponentielles, j'ai un DM à faire et je n'y arrive pas.
But : Pouver que lim x
+
ex/x = +
1- Justifier que pour tout x>0, on a l'équivalence suivante :
ex/x > x 
ex-x² > 0
2- Soit la fonction définie sur [0;+[ par f(x)= ex-x²
Justifier que f est deux fois dérivable sur [0;+[. Calculer f"(x), où f" est la dérivée seconde de f.
3- a) Justifier que l'équation ex=2 a une solution et une seule sur [0;+[
b) On note cette solution 
. Déterminer un encadrement d'amplitude 10-3 du nombre
c) Justifier que sur [0;[, on a ex< 2 et que sur ];+[, on a ex > 2
Voilà alors j'ai pas réussi grand chose juste :
1- j'ai mis :
ex/x > x
ex > x²
ex-x² > 0
2- j'ai trouvé :
f(x)= ex-x²
f'(x)= ex- 2x
f"(x)= ex- 2
Mais je suis pas sur de mes réponces
Pouvez vous m'aider ? car je suis vraiment mal partie 
Merci d'avance
ok je vous merci.
Mais je ne vois pas comment dire que f est 2 fois dérivable sur [0;+[
car je pensais qu'à la calculette que f(x) aurai 2 solutions à 2 endroits différents mais il se trouve que non.
J'espere que vous avez compris mon explication.
Mais je ne vois pas comment dire que f est 2 fois dérivable sur [0;+[
car je pensais qu'à la calculette que f(x) aurai 2 solutions à 2 endroits différents mais il se trouve que non.
J'espere que vous avez compris mon explication.
Absolument pas.
Je ne vois pas le rapport entre "2 fois dérivable" et "a deux solutions".
Sur quelle question travailles-tu en ce moment ?
Elle est même infiniment dérivable, comme somme de fonctions infiniment dérivables, l'exponentielle et un polynôme.
ah oui merci je viens de comprendre 
je suis entrain de faire le 3- a)
je vous mettrai demain ce que j'ai réussi à faire (car je viens de retrouver un exercice semblable à la 3 a) que j'ai fait en cours)
je vous dirai ça demain vers 15h.
J'espere que vous serez là pour regarder si c'est juste ou pas.
Merci.
Alors voilà ce que j'ai trouvé :
3- a) ex> 0 et ex est strictement croissante sur [0;+[
Donc ex= 2 a une solution et une seule sur [0;+[
b) D'après le tableau des valeurs de la calculatrice on obtient :
x y
0,693 1,9997
> < 2
0,694 2,0017
Donc 0,693<< 0,694
c) Parcontre là je ne sais pas comment justifier car on sait que < 0,694 donc ex< 2 mais je n'arrive pas à expliquer.
Vous pourriez me dire comment faire pour justifier et si ce que j'ai mis avant est juste ou pas ? (j'espere que c'est bien expliquer)
Merci.
3a) ton explication ne suffit pas.
Théorème des valeurs intermédiaires
exp continue e^0=1 et e^2=B avec B > 3 (j'ai pris e^2>3, j'aurais pu prendre e^10>1000, c'est pareil il faut juste que l'argument soit pertinent) et donc pour toute valeur V entre 1 et B, il existe au moins une valeur X entre 0 et 3 tel que exp(X)=V
en posant V=2 qui est effectivement situé entre 1 et B :
il existe au moins une valeur A entre 0 et 2 telle que e^A=2
3c)
exp(x) croissante, donc x<A --> exp(x)<exp(A), x>A --> exp(x)>exp(A)
Merci pour ton explication.
Suite de mon DM :
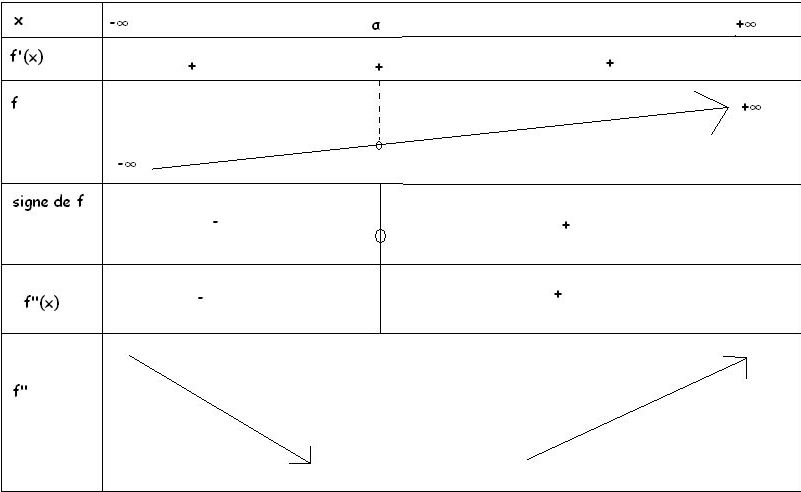
4a) Dresser le tableau de signes de f"(x)
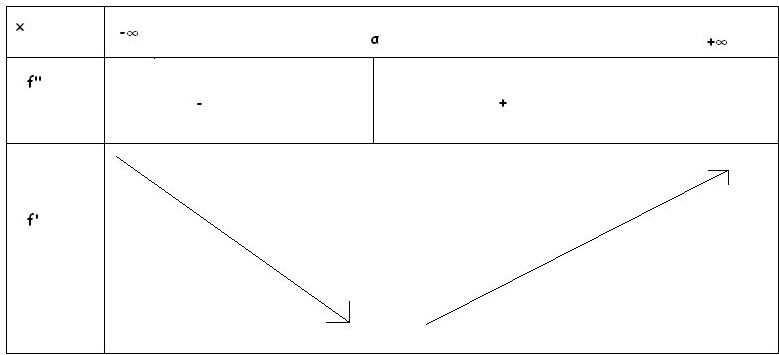
b) En déduire le sens de variation de la fonction f'
voilà se que j'ai fait
désolé se que j'ai fait (piece joint) :
1er tableau : 4-a)
2eme tableau 4b)
Pouvez vous me dire si cela est juste ?
J'ai des problemes aussi pour les questions suites :
c) Montrer que f'()=2(1-) et justifier que f'()>0
Pour cette question je vois pas du tout comment faire :s
d) Calculer f(0)
f(x)= ex - x²
f(0)=e0- 0²
f(0)= 1
Dit moi si la d) est juste ?
f) Prouver à l'aide des résultats précédents que pour tout x de [0; +[, on a f(x)>0
Je justifie comment ?
Voilà j'espere que mes tableau de variations sont bons aussi.
Merci d'avance de m'aider.
Annuler
connectez vous