Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. SecondeForum de Maths Seconde Équations et inéquationsTopics traitant de équations et inéquations [tout]Lister tous les topics de mathématiques
Niveau seconde
Partager :

DM Pyramide de Khéops

Posté par
Coconutjuice 20-04-11 à 16:22

Bonjour,
alors voilà, je bloque sur cet exercice.. J'éspère que je trouverais de l'aide ici.;

Problème :
La Pyramide de Khéops, située en Egypte, est a base carrée de côté 230 mètres (à quelques cm près..)
A l'origine, elle était composée de 212 étages de 69cm de haut chacun.
De combien d'étages au moins faut-il monter pour faire le tour complet de la pyramide sur un même niveau en parcourant moins de 100 mètres ?
Vous réaliserez notamment un patron à l'échelle 1/3000ème.
Si j'ai bien compris, il faut trouver à quel étage on peut faire un tour complet de la pyramide en parcourant moins de 100mètres ?
Pour le patron je pense me débrouillée..

Merci d'avance !

Posté par
Hiphigeniere : DM Pyramide de Khéops 21-04-11 à 08:37

Bonjour Coconutjuice

Tu connais la hauteur de la pyramide : 219*0,69 = 146,28m.
Le périmètre du nième étage doit être inférieur à 100m. Le côté c de cet étage sera alors inférieur à 25m.

Tu appliques Thalès sur base de ce dessin.
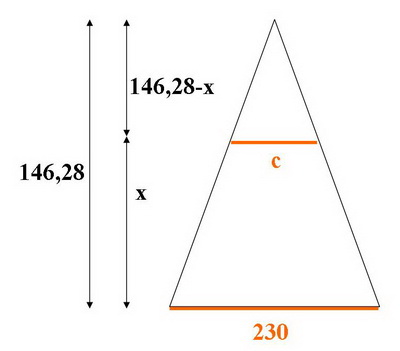
DM Pyramide de Khéops

\rm \fr{c}{230} = \fr{146,28-x}{146.28}

\rm c = \fr{230(146,28-x)}{146.28}

En résolvant l'inéquation \rm \fr{230(146,28-x)}{146.28} < 25, tu peux trouver x.

Il suffira alors de diviser par 0,69 pour avoir le nombre d'étages correspondant.

Posté par
Coconutjuicere : DM Pyramide de Khéops 24-04-11 à 11:53

Bonjour Hiphigenie,
Merci beaucoup pour ton aide !
Je n'avais pas du tout pensé à mettre les cm en m, je comprend pourquoi je trouvais mes résultats bizarre !
Donc pour l'équation, je fais :
\frac{(33644,4-230x)}{146,28}< 25
33644,4-230x < 25 \times (-146,28)
-230x < 25 \times (-3657) - 33644,4
-230x < -37301,4
x < \frac{-37301,4}{-230}
x < 162,18

ou je me trompe .. ?
si c'est ça, c'est 162,18 que je divise par 0,69 ? (ça tombe pas juste, et en plus ca fait 235 alors qu'il y a 212 étages.., je crois que j'ai besoin d'aide pour l'équation aussi )

Posté par
Hiphigeniere : DM Pyramide de Khéops 24-04-11 à 12:15

Citation :
\rm 33644,4-230x < 25 \times (-146,28)
Attention...

Il s'agit de \rm 33644,4-230x < 25 \times\ 146,28.

Pour éliminer le dénominateur, on multiplie les deux membres par 146,28

Posté par
Coconutjuicere : DM Pyramide de Khéops 24-04-11 à 12:24

donc je met "x146,28" des deux côtés ?

Posté par
Coconutjuicere : DM Pyramide de Khéops 24-04-11 à 12:35

je fais

33644,4 - 230x < 25 \times 146,28

-230x < 3657 - 33644,4

-230x < -29987,4

x < \frac{-29987,4}{-230}

x < 130,38

?

Posté par
Hiphigeniere : DM Pyramide de Khéops 24-04-11 à 12:39

\rm \frac{(33644,4-230x)}{146,28} < 25

\rm \frac{(33644,4-230x)}{146,28} \times\ 146,28 < 25 \times\ 146,28

\rm 33644,4-230x < 25 \times\ 146,28

\rm 33644,4-230x < 3657

\rm -230x < 3657 - 33644,4

\rm -230x < -29987,4

\rm x > \fr{-29987,4}{-230}

Attention, ici le sens de l'inégalité a changé car on a divisé l'inéquation par -230 qui est négatif.

Posté par
Hiphigeniere : DM Pyramide de Khéops 24-04-11 à 12:51

Donc x > 130,38 (mètres).

Chaque étage mesure 0,69 m.

Cela correspond alors à combien d'étages ?

Posté par
Coconutjuicere : DM Pyramide de Khéops 24-04-11 à 12:56

ah oui d'accord.
donc du coup
x > 130,38
et je fais \frac{130,38}{0,69}  ?
ca tombe pas juste ca fait environ 188,95.
Donc c'est au 189ème étage qu'il faut être ?

Posté par
Hiphigeniere : DM Pyramide de Khéops 24-04-11 à 13:22

Posté par
Coconutjuicere : DM Pyramide de Khéops 24-04-11 à 13:59

oh super merci !
Je pourrais te montrer mon patron quand je l'aurais fini ?

Posté par
Hiphigeniere : DM Pyramide de Khéops 24-04-11 à 14:53

J'espère qu'il sera correct

Posté par
Coconutjuicere : DM Pyramide de Khéops 24-04-11 à 22:16

alors voila, pour le patron à l'échelle 1/3000ème, j'ai fait :
230m = 23000cm
\frac{23000}{3000} 7,6 cm

et, 146,28m = 14628 cm
\frac{14628}{3000}= 4,876

Donc 4,876 ca représente bien la hauteur et non pas le côté du triangle ?

voilà mon patron :

DM Pyramide de Khéops

Posté par
Hiphigeniere : DM Pyramide de Khéops 24-04-11 à 22:56

Attention, les 146,28m représentent la hauteur de la pyramide et non pas la hauteur du triangle.

La hauteur de la pyramide est en bleu et la hauteur du triangle à dessiner est en rouge.
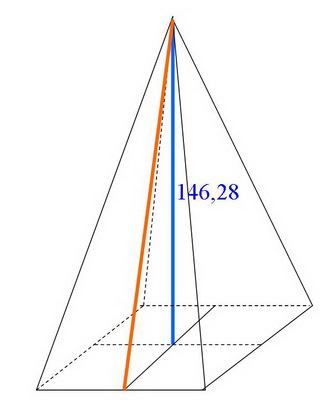
DM Pyramide de Khéops

Il faut calculer cette hauteur en rouge par Pythagore.

Posté par
Coconutjuicere : DM Pyramide de Khéops 25-04-11 à 20:23

ah d'accord !
je l'ai refait, je me suis aidé de ton triangle, j'ai placé A sommet de la pyramide, C le milieu de la pyramide, et B le milieu d'un coté de la pyramide.
(BC = \frac{230}{2} = 115 )

Donc ca donne : dans le triangle ABC rectangle en C, on a d'après les théorème de pythagore :

AB² = AC² + BC²
AB² = 146,28² + 115²
AB² = 34622,8384
AB = 34622,8384
AB = 186,0721322 186,1m

et pour l'échelle :
186,1m = 18610 cm
\frac{18610}{3000} 6,2 cm

DM Pyramide de Khéops

Posté par
Hiphigeniere : DM Pyramide de Khéops 25-04-11 à 21:25

Ca, c'est plus correct ...

Posté par
Coconutjuicere : DM Pyramide de Khéops 25-04-11 à 21:45

merci beaucoup pour ton aide !!

Posté par
Hiphigeniere : DM Pyramide de Khéops 25-04-11 à 22:38


Rechercher
Menu
Espace membre
10 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1742 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !