Inscription / Connexion Nouveau Sujet
dm seconde
Bonjour, j'ai commencé à faire cet exercice mais je suis maintenant coincée, si quelqu'un pouvait me donner un coup de main et m'expliquer, merci beaucoup.
On donne dans un repère orthonormé (unité 1cm), les points A(2;-1), B(5;0) et C(1;6).
1) Réaliser une figure que l'on completera au fur et à mesure de l'exercice.
2) Déterminer une équation de la droite (AB).
3) Soit d1 la médiatrice de [AB].
a) Justifier que : M(x;y) \epsilon d1 si et seulement si MA=MB.
b) En déduire une équation de la droite d1.
4) En déduire une équation de la hauteur d2 issue de C du triangle ABC.
5) Déterminer alors les coordonnées du point H, point d'intersection de la hauteur d2 et de la droite (AB).
6) Calculer l'aire du triangle ABC.
Où j'en suis ?
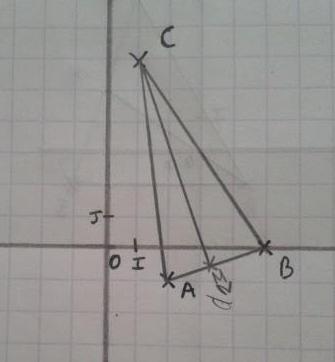
1) (Voir image en lien)
2) L'équation de la droite (AB) est y = 1/3x - 5/3
Mais pour le reste, je ne sais pas quoi faire du tout... 
3) Soit d1 la médiatrice de [AB].
a) Justifier que : M(x;y) \epsilon d1 si et seulement si MA²=MB²
si un point appartient à la médiatrice d'un segment, alors ce point est équidistant des extrémités de ce segment--> MA=MB--> MA²=MB²
b) En déduire une équation de la droite d1.
calcule MA² et MB²
rappel de cours : AB²=(xa-xb)²+(ya-yb)²
Bonjour CindyXx
je ne suis pas d"accord avec ton dessin
il n'y a pas de raison que M soit le milieu de [AB]
tu as vu (en 6e ) 
qu'un point appartient à la médiatrice de [AB] équivaut à dire que MA=MB (ce n'est pas simplement une implication, c'est une équivalence), c'est ce qu'on appelle une propriété caractéristique, c'est à dire une propriété qui caractérise la médiatrice du segment
les coordonnées de M, le texte les a appelées (x;y)
en écrivant que MA²=MB², tu vas trouver une relation entre le x et le y de M, et ça, c'est ce qu'on appelle une équation de la droite...
à toi, vas -y
malou Si je comprend bien, je dois calculer l'équation de la droite d1, enfin c'est la question ! Mais en prenant les coordonnées de quels points ? 
en écrivant que la distance MA=la distance MB
amis dans une formule de distance, il y a les grandes racines carrés
OK ?
donc on préfère dire
MA²=MB² car les distances étant des valeurs positives, on peut écrire qu'elles sont égales ou que leurs carrés sont égaux ce qui revient au même
donc calcule MA²
calcule MB²
et écris que MA²=MB² tu vas trouver ton équation de médiatrice après simplification
malou D'accord donc la formule à utiliser est MA^2 = (xa-xm)^2 + (ya-ym)^2, mais comment dois-je faire pour trouver les coordonnées de M ? Je dois garder (x;y) ?
oui, c'est ça
et tu gardes (x;y), oui, bien sûr
fais le
simplifie
et tu vas voir, à la fin de ton calcul, tu vas bel et bien trouver une équation de droite
malou Par exemple pour
MA^2= (xA-xM)^2 + (yA-yM)^2
= (2-x)^2 + (-1-y)^2
=
MB^2 = (5-x)^2 + (-y)^2
Mais là je bloque pour la fin des calculs...
non, tu fais des erreurs de signe entre autres
MA²=MB²
(2-x)²+(-1-y)² = (5-x)²+(-y)² ça OK
remarque : (-1-y)² =(1+y)² car un nombre et son opposé ont le même carré
à droite, je ne vois pas d'où tu as fait sortir le -2y
réessaie à partir de là : (2-x)²+(-1-y)² = (5-x)²+(-y)²
oubli du carré sur le dernier y de ta ligne
c'est y²
oui, cette fois impeccable
vas-y, simplifie les x², les y²
et le reste, écris le un peu mieux
tu devrais pouvoir arriver à une écriture du type y=ax+b
malou Mais juste, sur la figure, du coup, ou dois- je placer le point M car j'ai oublié de te demander pourquoi tu n'étais pas d'accord !
parce qu'il y a une infinité de point M, puisque ce sont tous les points de la médiatrice
donc je ne veux pas voir le point M juste au milieu du segment [AB] faisant croire qu'il n'y a qu'un seul point qui répond à la question
oK ? tu comprends ?
malou A d'accord, mais d1 passe quand même par le milieu de [AB] puisque c'est une médiatrice. et le M peut se situer à nimporte quel endroit sur d1, c'est ça ?
Et du coup, pour la question 4, l'équation de la hauteur d2 est la même que d1 non ?
oui, je m'absente parfois, mais je reviens toujours...
alors M, n'importe où sur D1, oui
mais D1 ne passe pas par C, si ? je ne le pense pas
ton triangle ABC ne me semble pas isocèle
auquel cas la hauteur n'est pas confondue avec la médiatrice
mais ce sera une droite //
ça servira de le savoir pour déterminer une équation de la hauteur
malou D'accord, mais quelle est la formule pour pouvoir calculer l'équation de la hauteur sachant que celle-ci est // avec la médiatrice et q'elles possèdent donc pour coef directeur -3 ? 
oh...
tu pars de y=ax+b
mais tu connais son coeff directeur -3
donc
y=-3x+b
maintenant, utilise le fait que tu sais que la hauteur passe par C dont tu connais les coordonnées...
OK ?
malou
On sait que l'équation de (d2) est de la forme y=ax+b
De plus, (d2)//(d1), donc elles ont le même coefficient directeur qui est de -3.
Donc l'équation de la droite est de la forme y=-3x + b
C(1;6) appartient à (d2)
6 = -3 X 1 + b
6= -3 + b
9 = b
Donc l'équation de (d2) est de la forme y = -3x + 9
C'est bien ça ?
malou
Pour la question 5
On donne les droites d'équations :
(d2) d'équation y=-3x+9 et
(AB) d'équation y= 1/3x - 5/3
Les deux droites ne sont pas parallèles car les coefficients directeurs ne sont pas les mêmes.
On résout le système :
y=-3x+9
y=1/3x-5/3
y=-3x+9
9y=3x-15
y=-3x+9
10y=-6
y=-3x+9
y=-6/10
-6/10=-3x+9
y=-6/10
-6/10-9=-3x
y=-6/10
-48/5 = -3x
y=-6/10
(-48/5)/(-3)=x
y=-6/10
x=-16/5
y=-6/10
Donc H( -16/5 ; -6/10 )
malou
Cool ! Juste une petite dernière question pour la 6)
Je sais que pour calculer l'air d'un trinagle c'est base × hauteur, mais du cp, comment faut-il calculer ? Pck il faut multipler AB × d2... Mais comment trouve t'on les longueurs ? En calculant la distance ?
eh oh...faut pas oublier d diviser par 2 pour avoir l'aire d'un triangle....
oui, les longueurs, tu calcules avec la formule de la distance entre deux points
longueur=distance
malou
Oui en effet !
AB2 = (5-2)2+(1)2
= [...]
= 10
HC2 = (1-16/5)2 + (6+6/10)2
= [...]
= 242/5
Aire ABC = (10 X 242/5) / 2 = 242 cm2
C'est bien cela ?
attention, ce sont les carrés des distances et non la distance
pour la 2e, je trouve 234/5 et non 242/5
malou
Euh, je n'ai pas compris, du coup ce qu'il fallait changer :/
Je n'arrive pas à tomber sur 234/5 !
tu as calculé AB²
AB²=10
donc
AB=
10
pour l'autre, honte à moi, j'ai dit que 5-11 = -9 !!!!!!
c'est toi qui a raison avec 242/5
mais même chose c'est le carré
donc tu dois prendre la racine carrée
oK ?
malou
Ah d'accord, donc alors si on fait avec les racines carrées, on trouve une aire de 11 cm2
Pas de soucis ! 
malou
Ah oui ! En tout cas je te remercie énormément d'avoir passer autant de temps à m'expliquer cet exercice, c'est très sympa 
Annuler
connectez vous