Inscription / Connexion Nouveau Sujet
Donner les variations de la fonction
Bonjour qui pourrait m'aider je suis perdu
** image supprimée **
Bonjour
tu n'as pas respecté le règlement du site
recopie ton énoncé en réponse à mon message
et dis ce que tu as commencé à chercher
ensuite nous t'aiderons
Bonjour actuellement j'ai effectué la dérive de g(x) qui est g'(x)=-1 +e^x mais par la suite je n'ai pas trop compris comment faire ?
** image supprimée **
*** message déplacé ***
)
Bon...la première fois j'explique, la 2e fois je sévis
la FAQ du forum
) :
On considère la fonction f définie et dérivable sur l'ensemble R des nombres réels par :
f(x) = x + 1 +x/e^x
On note C sa courbe représentative dans un repère orthonormé (0, I,J).
1) Soit g la fonction définie et dérivable sur l'ensemble R par: g(x) = 1 - X+e^x
Dresser, en le justifiant, le tableau donnant les variations de la fonction g sur R.En déduire le signe de g(x)
limites de g aux bornes de son ensemble de définition ne sont pas attendues). En déduire le signe de g(x).
2) Déterminer la limite de f en -infini puis la limite def en +Infini,
Actuellement je n'ai que effectué la dérivée de g'(x)=-1+e^x pour le reste je ne pas quoi faire
*** message déplacé ***
faut pas abuser
tu es banni 1 heure
ainsi tu liras peut-être le règlement
Sujet ancien- ne plus donner ce lien-merci
et
[lien]
f(x) = x+1+x/ex
g(x)=1-x+e^x
g'(x)=-1+ex
3) On appelle f' la dérivée de la fonction f sur R. Démontrer que, pour tout réel x, f'(x) = e-*g(x)
Je voudrais bien une petite aide je ne trouve pas
*** message déplacé ***nouveau multipost...tu le fais exprès ?
tu n'as pas répondu à la question 1
pour le moment tu n'as calculé que la dérivée, qui est juste, mais ce n'est pas fini
bonjour,
peux tu préciser f(x) ? c'est f(x) = x + 1 + x/e^x ?
montre ce que tu as fait pour calculer f'(x) ?
et précise aussi ton énoncé : "Démontrer que, pour tout réel x, f'(x) = [b]e-*g(x)[ ?? /b]"
Bonjour hekla justement en fesant le calcul je suis tombé sur le corrigé mais j'essaye de comprendre comment mais je n'arrive pas appliquer u/v ou plutôt que a la fin je trouve le mauvais résultats
Bonjour cava être compliqué de préciser l'énoncé car l'énoncé est décrit mot pour mot
et que j'ai du mal à comprendre
Bon reprenons
est une fonction définie sur
par
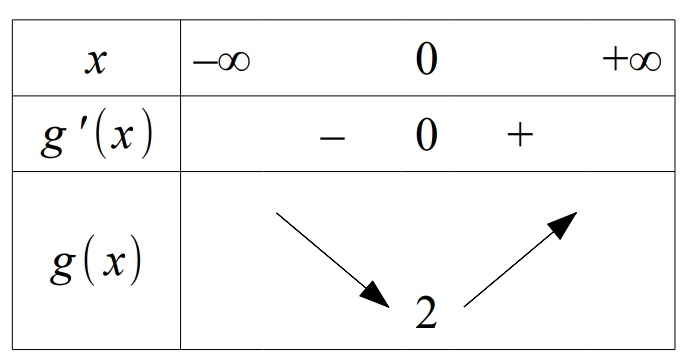
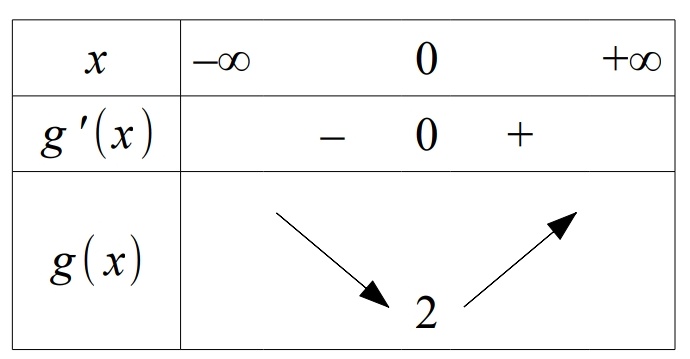
Vous avez donc trouvé que et les réponses à la question 1 se sont arrêtées là. Quel est donc le sens de variation de
et le signe de
?
Question 2 on supposera que est définie par
est donc de la forme
la dérivée sera alors
On a donc posé
d'où
Bonsoir Leile
Ah ok merci beaucoup je comprends mieux
Pour le signe et le Sens de variation puis je vous montrez mes travaux via une photo ?
Non le scan des brouillons ne sont pas admis sur ce forum Si vous le faites vous risquez d'être banni pour un peu plus longtemps
Vous pouvez joindre un tableau de cette sorte rempli, mais c'est tout.
Il faut mettre des parenthèses
Oui Après il faut mettre les questions, mais avant il vous restait les limites à faire
Sur le site j'utilise
Dans sous la feuille de réponse vous trouvez les symboles
Quelles étaient les autres questions ?
Les autres questions étaient
En déduire le tableau de variation de la fonction f'sur R
Demontrer que l'équation /tx=0 admet une unique solution réelle x sur R Démontrer que -1<x-0.
Mais je ne les ai pas encore abordé
Il faut sans doute lire l'équation admet une unique solution réelle
sur
Démontrer que
signe de et sens de variation pas de problème
théorème des valeurs intermédiaires ?
ça et non sa
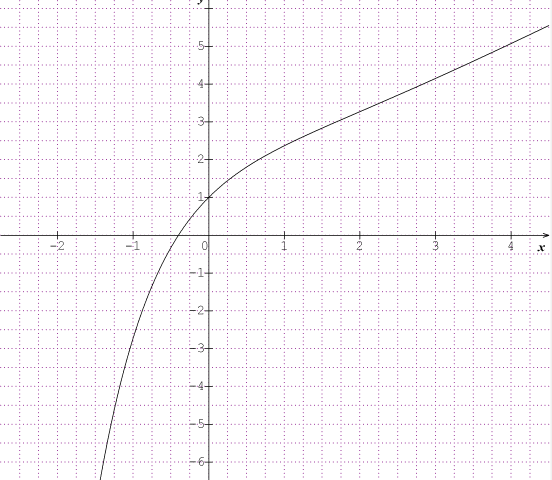
Rebonjour j'aurais juste une question comment faire pour une questions on a vu ça très vaguement en cours
Démontrer que la droite T d'équation y=2x+1 est tangente a la courbe C au point d'abscisse 0.
Sa fait f(0)=1 et f'(0)=g(0)2
Donc y-1=2(x-0)
T=y=2x+1
Mais le problème se pose pour cette question
Étudier la position relative de la courbe C et de la droite T.
Comment faire ?
Bonjour
tu as une fiche qui traite de la position : Etude de la position relative de deux courbes
Annuler
connectez vous
Dérivées en terminale