Plein de manières de faire.
Il faudrait que tu précises un peu ton exercice qu'on discute sur un cas pratique.

En fait il y a un triangle rectangle dont le côté adjacent à l'angle droit est de x+4. l'autre côté adjacent à l'angle droit est aussi le côté d'un rectangle dont la valeur est (x/2) -1. enfin la longueur du rectangle est x.
le but est de comparer les aires du triangle et du rectangle en fonction de la valeur de x.

Je ne sais pas ce que c'est que la longueur d'un rectangle. Veux-tu parler de son périmètre ?

Donc je traduis :

ABC triangle, rectangle en A



Rectangle ACDE
périmètre du rectangle

Est-ce que ça ressemble à ça ?



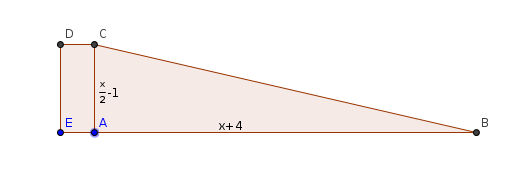
Si les noms des points ne correspondent pas avec ton exercice, évite de me le faire remarquer. Tu traduiras toi-même.

oui la figure c'est exactement ça, sauf que x c'est la longueur EA. donc je cherche comment donner des valeurs aux longeueurs.

triangle rectangle
côté adjacent à l'angle droit est de x+4.
autre côté adjacent à l'angle droit est aussi le côté d'un rectangle dont la valeur est (x/2) -1.
la longueur du rectangle est x.

Donc je reformule. Mais pitié, apprends à être un peu plus précise dans tes propres exposés. Il y a une certaine distance entre ta première expression :
la longueur du rectangle est x
et l'information qui arrive seulement maintenant,
EA=x

Donc on imagine, en dehors de toute autre indication, que tu veux réaliser sous GeoGebra une figure comme celle de mon premier schéma, et pouvoir déplacer le point E, car c'est lui qui donne la valeur à la variable appelée x dans ton énoncé et dont dépendent les autres points et figures du problème.

D'abord, que connais-tu de GeoGebra ? Quelle expérience en as-tu ?
Si je parle de la barre de formule, de l'outil Polygône, est-ce que ça évoque des choses précises ?

Ou alors faut-il que je parte du principe qu'en fait tu n'as jamais manipulé et que tu pars de 0 ?

j'utilise Geogebra depuis septembre 2010 donc je connais un peu. je sais faire une figure simple, utiliser les fonctions polygones, vecteurs etc...

Ok, alors c'est parti.

Aujourd'hui, on ne va pas se contenter de placer avec l'outil "Point" des points sur la surface de dessin, on va leur donner des coordonnées.
Parce que GeoGebra fait tout par calcul, et qu'on veut lui imposer de faire certains calculs.

Alors la solution que je vais te proposer n'est peut-être pas la plus élégante, j'espère qu'elle va être pour toi simple à appréhender.

D'abord, on imagine (c'est un choix qu'on fait) qu'on veut
- placer un point A qui ne bougera pas
- placer un point E sur l'horizontale qui passe par A, et qu'on pourra faire bouger, mais seulement sur cette horizontale.
- placer ensuite les autres points pour qu'ils respectent les longueurs et dispositions imposées par l'énoncé.

Quand tu ouvres GeoGebra, tu vois apparaitre deux premières droites graduées, les axes d'un repère orthonormé. Si ce n'est pas le cas, affiche les grâce au menu "Affichage/axes".

On choisit de placer le point A à l'origine de ces axes.
Pour cela, on va saisir dans la barre de formule, sous la surface de dessin, l'expression suivante :
A=(0,0)
Remarques : dans GeoGebra, le séparateur de liste n'est pas le ; mais la ,
et le séparateur décimal est le .

Ainsi, l'expression A=(0,0) indique à GeoGebra qu'il doit créer un point nommé A, de coordonnées 0 pour son abscisse, et 0 pour son ordonnée.

Pour créer le point E, ça va être encore plus sportif :
on va lui indiquer qu'il lui faut placer le point sur cette horizontale qui est en fait l'axe des abscisses.
Dans GeoGebra, cet axe est appelé axeX
Attention : GeoGebra fait la distinction entre minuscules et majuscules. si tu lui dit axex, il ne comprendra pas.

Donc pour créer le point E, on lui dit :
E=Point[axeX]

Tu remarqueras que quand tu commence à taper une commande, GeoGebra te propose de la compléter.
Ainsi, quand tu saisis
E=poi
GeoGebra te propose obligeamment de terminer pour toi la saisie, en surlignant la suite de ce qu'il croit deviner
E=point[]

tu peux alors saisir
E=poi
suivi d'un appui sur la touche "Entrée" de ton clavier.
Tu te retrouve dans les crochets [|] et tu peux alors saisir axeX

Tu vois alors apparaitre un infâme gribouillis à l'origine du repère.
C'est parce que GeoGebra a créer initialement le point E au même endroit que le point A

Avec la souris, sélectionne le point E en enfonçant sans le relâcher le bouton normal (gauche) de ta souris sur le gribouillis en question. Puis déplace la souris, sans relâcher le bouton, et tu verras le point E se déplacer de même.

On fait déjà ça.

C'est bon, j'arrive à faire le début.
merci, je ne savais pas qu'on pouvait faire comme ça.

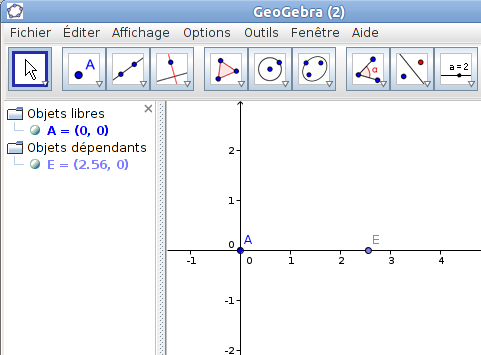
Tu remarqueras que le point E peut se déplacer sur tout l'axe des abscisses, ce qu'on ne souhaitait pas dans l'objectif initial.
Pour l'instant, on lui laisse cette liberté, on corrigera plus tard.

Maintenant, on va créer la longueur x de quoi dépend tout le reste.

Mais attention : on ne peut pas la nommer x, car c'est une fonction réservée de GeoGebra, qu'on va rapidement utiliser d'ailleurs.

Donc on va appeler cette longueur d'un autre nom. Choisissons 'm', c'est souvent la lettre utilisée dans les problèmes avec paramétrage.

Et nous allons, toujours dans la barre de formules, saisir la commande suivante :
m=Distance[A,E]

Maintenant, à toi de travailler : tu vas créer, grâce à la barre de formule, les points B et C et D si tu t'en sens la capacité.

Pour cela, il te faut exprimer les coordonnées de B et C (et D) en fonction de m (et non plus de x)

A toi !

j'ai réussi!
merci beaucoup, vraiment.
Demain en cours j'aurai tout compris à l'exercice.

merci

Je n'avais pas l'impression que cela devait se terminer aussi rapidement.
Eh bien tant mieux ou tant pis.
Bonne continuation.