Inscription / Connexion Nouveau Sujet
Droite remarquable d'un triangle
Bonjour, j'ai un dns de mathématiques à faire mais je suis bloquée ..
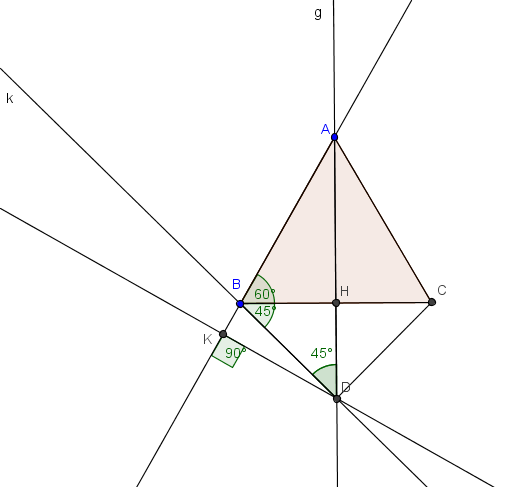
" ABC est un triangle équilatéral de côté 2 et BDC est un triangle rectangle isocèle en D.
1. Démontrer que la droite (AD) est perpendiculaire à la droite (BC). On note H leur point d'intersection.
2. Soit K le pied de la hauteur issue du triangle ADB. Calculer KD en fonction de sin15° .
3. Calculer l'aire du triangle ABD.
4. A l'aide des questions 2 et 3, démontrer que la valeur exacte de sin15° est
(  6-
6- 2 ) : 4 . "
2 ) : 4 . "
La question est déjà faite :
1. [...] Donc la droite (AB) est médiatrice au segment [BC] et (AB) est perpendiculaire à (BC).
La question 2 est commencée :
2. On a prouvé que ABC=BAC=ACB=60°, que DBC=DCB=45° et que ABD=15°.
Ensuite je suis bloquée, je n'arrive plus à rien ..
Merci d'avance 
bonjour loulou910
Soit K le pied de la hauteur issue du triangle ADB
elle est issue de quel sommet cette hauteur s'il te plaît ....
analyse ta figure, on connait plein de choses !
question 2 : dans BKD, tu peux connaitre B puis D
d'où le 15°
et sinus = opposé/hypoténuse
aire (ABD) = base*hauteur relative*1/2
tu n'as pas le choix je crois
base = AD
hauteur = BH
allez, vas-y !
Oui j'ai compris merci 
Pour le petit 2) : j'ai prouvé que ABC=BAC=ACB=60°, que DBC=DCB=45° et que ABD=15°.
Dans le triangle CBD, rectangle en D :
cosDBC=BD/BC
cos45°=BD/2
BD=2 x cos 45°
BD=1,4
Donc BD mersure 1,4
Dans le triangle KBD, rectangle en K :
sinKBD=KD/BD
sin15°=KD/1,4
KD=1,4 x sin15°
KD=0,4
Donc KD mesure 0,4
Pour le petit 3) :
Dans le triangle ABC, on sait que K est le pied de la hauteur issue de D.
Aire ABC= AB x DK /2 = 2 x 1,4 /2 = 1,4
Donc l'aire du trianble ABC est 1,4 .
Par contre, pour le petit 4) je sèche ..
dis moi, est ce que toi tu avais une figure avec l'énoncé ?
car le point D, rien ne dit qu'il est en dehors du triangle ABC comme je l'ai fait
il aurait pu être aussi au dessus de (BC) donc être dans le triangle ABC, et là à mon avis ça va mieux !....car dans ta démonstration avec la figure que je t'ai envoyée, le sinus n'est pas bon....
je regarderai ta réponse ce soir pour le problème de figure
ouaou.....fallait le dire !....donc tu oublies ma figure !
donc dans ton post d'hier, en gros c'est ça, mais surtout garde les valeurs exactes
du genre sin15 = KD/BD donc KD =  2 sin15
2 sin15
ensuite : aire (ABD) = AB*KD = 2 2 sin15
2 sin15
mais aire (ABD) = aussi
= aire(ABH) - aire (BHD) continue..., calcule
et écris que les deux aires sont égales, tu vas trouver la valeur de sin15 donnée dans l'énoncé....


