Inscription / Connexion Nouveau Sujet
ecrire des expressions sous la forme d'un quotient
Bonjour, pouvez-vous m'aider svp.
a) Ecrire chacune des expressions sous la forme d'un quotient, après avoir précisé les valeurs interdites.
E= 3- 5/(x¨2+2)
F= (1/x)-(5x+2/x+1)+1
Pour la E j'ai déjà fait quelque chose mais je ne pense pas que ce soit fini.
E= (3(x^2+2)/x^2+2) - (5/x^2+2)
E= 3x^2+6-5/x^2+2
E= 3x^2+1/x^2+2
Merci d'avance, parce que je suis perdue là.
Salut,
La E a l'air correcte, il faut être sûre de toi 
Tu as bel et bien donné l'expression sous la forme d'un quotient après tout, non ?
Par contre, tu n'as pas fini pour la E : tu dois aussi préciser les valeurs interdites, c'est-à-dire que vu qu'on n'a pas le droit de diviser par zéro,
On doit avoir : x2 + 2  0, tu vois ?
0, tu vois ?
En résolvant ça (fais comme si le  était un = ça marche pareil), tu trouveras la ou les valeurs interdites
était un = ça marche pareil), tu trouveras la ou les valeurs interdites 
Et puis ben t'as plus qu'à faire pareil pour la F ^^
Merci énormément c'est parce que je pensais qu'on ne devait pas laisser de carré. Mais pour la valeur interdite, il n'y en a pas vu que les carrées sont toujours positifs. Et pour le F, voilà ce que h'ai fait:
F= (1/x)-(5x+2/x+1)+1
F= 1(x+1)/x(x+1) - (5x+2/x+1) + (1(x+1)/x+1
F= 1(x+1)/x(x+1) - 6x+3/x+1
F= x+1/x(x+1) - x(6x+3)/x(x+1)
F= x+1-6x^2+3x/x(x+1)
F= -6x^2+4x+1/x^2+x
Voilà, est-ce juste svp?
Voilà ! Très bien pour la fin du E tu dois quand même préciser qu'il n'y a pas de valeur interdite même si ça te paraît évident, c'est quand même une partie de la question 
Ben pour savoir si ton F est juste, tu fais un truc simple : tu essayes quelques valeurs de x et tu regardes si tu obtiens le même résultat avec la formule de départ et celle d'arrivée.  Ou alors tu tapes sur ta calculette la première forme de F et tu regardes le graphe, puis tu effaces et tu tapes ton résultat final tu es censée avoir le mpeme graphe si c'est correct ^^
Ou alors tu tapes sur ta calculette la première forme de F et tu regardes le graphe, puis tu effaces et tu tapes ton résultat final tu es censée avoir le mpeme graphe si c'est correct ^^
Tout ça te servira en devoir pour être sûre de tes résultats.
Bon, je vais pas faire durer le suspense plus longtemps : c'est... presque bon 
J'ai volontairement laissé x(x+1) au dénominateur puisque tu dois encore trouver les valeurs interdites, et cette forme est plus pratique pour les trouver. 
Merci beaucoup, vraiment ! c'est vraiment très gentil de prendre de votre temps pour m'aider.
Alors les valeurs interdites sont x=0 et x=-1
Cependant, désolée de vous déranger encore mais l'exercices n'est pas fini, il y a encore deux questions.
Etudier le signe de E selon les valeurs de x, justifier alors un encadrement de E
Etudier le signe de F selon les valeurs de x 
Pas de quoi 
Pour une étude de signe, tu as déjà fait des tableaux de signe ? Parce que c'est exactement ce qu'il faut faire ! 
Pour E et aussi pour F, tu étudies séparément le signe du numérateur, e signe du dénominateur, puis tu combines les deux !
Un très bon exemple ici : http://wims.unice.fr/wims/wims.cgi?session=RHB380B3FA.2&+lang=fr&+module=H6%2Fanalysis%2Fdocsignes.fr&+cmd=reply&+job=read&+foldin=fraction.3#primi3
(clique sur [Détails] de l'Exemple)
Oui je sais comment le faire mais pas avec des carrées.
3x^2+1=0 ssi x^2=-1/3
x^2+2=0 ssi x^2=-2
Mais les carrées me dérangent.
Pour F, sa donne:
-4x^2+1=0 ssi -4x^2=-1 ssi x^2=1/4 ssi x=1/2
x(x+1)=0 ssi x=0 ou x=-1
Voilà pour F sa semble marcher mais pas pour E.
Pour la E désolé de t'avoir induit en erreur, c'est en fait plus simple de faire le tableau de signes en partant de l'expression de base. 
Si tu étais en Première, tu aurais les outils mathématiques pour faire ça vite fait facilement ^^
Bon, donc on a
Comme tu le disais si bien, un carré est toujours positif. Donc au final, la seule chose qui va faire changer le signe de E, c'est de savoir pour quel x est-ce que est supérieur à 3 ! Si ça vaut pile 3, alors E vaut 0, si ça vaut moins de 3 alors E est positif et si ça vaut plus de 3 alors E est négatif.
Donc on résout : par exemple, la solution se trouve rapidement, et du coup on a trouvé la valeur de x qui fait changer le signe de E donc on peut construire le tableau de signe de E

Je sais pas si je suis clair ! Mais si je détaille plus je finis par tout te faire 
Je vois où vous voulez en venir, mais ça me parait très bizarre ce que j'ai trouvé:
5/x^2+2 (plus petit que) 3
5 (plus petit que) 2x^2+2
5-2 (plus petit que) 3x^2
3 (plus petit que) 3x^2
x^2 (plus grand que) 1
x (plus grand que) 1
Donc le E en gros, si je résous :
Ce qui est vrai pour tout x. Donc, pour tout x, , donc pour tout x, E > 0 puisque
!

E est positive sur ]- ;+
;+ [, c'est l'encadrement demandé, et la justification est la résolution de l'équation que je t'ai écrite juste précédemment;
[, c'est l'encadrement demandé, et la justification est la résolution de l'équation que je t'ai écrite juste précédemment;
Quant au tableau de signes, tu mets + partout, de - à +
à + , en fait c'est aussi simple que ça :
, en fait c'est aussi simple que ça :
x - +
+
E +
Tu n'as qu'à taper 3-5/(x^2+2) dans google pour t'en convaincre 
j'aurais juste une dernièere question et après je vous laisse tranquille . Pour la F: j'ai fait:
-4x^2+1=0 ssi x=1/2
x=0
x+1=0 ssi x=-1
sa ma donner le tableau déjà pour le produit x(x+1)
x - -1 0 +
-1 0 +
x - - 0 +
x+1 - 0 + +
x(x+1) + 0 - 0 +
et comme tableau final:
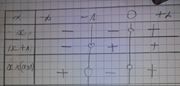
x - -1 0 1/2 +
-1 0 1/2 +
-4x^2 +1 + + + -
x(x+1) + 0 - + +
-4x^2+1/x(x+1)+ - + -
Pour ce qui est des valeurs intedites je les ai mises mais c'est difficile de le montrer là.

 1/4 ou -
1/4 ou -
