Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Géometrie plane et dans l'espaceTopics traitant de Géometrie plane et dans l'espace [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

écriture complexe ( isométrie)

Posté par
Hoffnung 31-03-21 à 23:49

Salut

Soit D le point tel que ABCD est un carré, et C le cercle circonscrit au carré ABCD.
A tout point M de cercle C distinct de A, on associe le point N de la droite (BC) tel que AM=CN et C \in\left[BN\right] .
On pose ( \vec{AB},\vec{AM})\equiv \alpha\left[2\pi\right]\alpha\in\left] \frac{-\pi}{4},\frac{\pi}{2}\right]   .


Soit f0 le déplacement qui envoie Aen C  et M en N .

1)Pour quelle valeur \alpha 0, f0 est une translation?( \alpha 0=\frac{-\pi}{2})

2) Le plan est muni du repère orthonorme direct (A,\vec{AB},\vec{AD}).

Pour \alpha\neq \alpha0 On note 0 le centre de la rotation f0 .

a) Montrer que ZN=ie^{-i\alpha }ZM+1+i
je peine a résoudre la question 2)a).

Merci d'avance.

Posté par
lakere : écriture complexe ( isométrie) 01-04-21 à 00:21

Bonsoir,

Dès le départ, la question 1) me parait bizarre.
De toute manière, tu sembles tomber sur un angle qui n'appartient pas au domaine indiqué par l'énoncé.

  

Citation :
Soit f0 le déplacement qui envoie Aen C  et M en N .


Avec cette définition, f_0 n'est pas une translation.

Posté par
Hoffnungre : écriture complexe ( isométrie) 01-04-21 à 00:42

c'est f\alpha je m'excuse. translation signifie que (\vec{AM},\vec{CN})\equiv 0\left[2 \pi \right] non? et j'intercale, \vec{AB} ça me donne\pi/2  est-ce que c'est correct ?

Posté par
lakere : écriture complexe ( isométrie) 01-04-21 à 00:45

Après réflexion, il semblerait que pour 1) il faille \alpha_0=+\dfrac{\pi}{2} auquel cas M est en D (en supposant ABCD direct)

2) z_M=re^{i\alpha}

    z_N=1+(1+r)i

Il suffit de vérifier la formule qu'on te fournit.
  

Posté par
lakere : écriture complexe ( isométrie) 01-04-21 à 12:28

Bonjour Hoffnung,

J'imagine que la suite de ton exercice consiste à :

   1) Trouver l'affixe du centre \Omega de la rotation (pas trop difficile).

   2) L'angle de cette rotation (plus délicat mais pour obtenir au final une expression fonction de \alpha très simple).

Pourrais-tu nous poster la suite de ton énoncé ?
Merci d'avance

Posté par
lakere : écriture complexe ( isométrie) 01-04-21 à 12:37

En fait, 2) n'est pas délicat du tout mais je m'y suis pris comme un manche

Posté par
carpediemre : écriture complexe ( isométrie) 01-04-21 à 14:27

saut

un énoncé bien imprécis ...

Hoffnung @ 31-03-2021 à 23:49

Soit D le point tel que ABCD est un carré, et C le cercle circonscrit au carré ABCD.
donc à priori A, B et C sont donnés ... mais comment ?

Posté par
Sylvieg Moderateurre : écriture complexe ( isométrie) 01-04-21 à 19:08

Bonjour,
Dans l'énoncé original, les lettres \; C \; sont peut-être différentes.

Pour ce qui est du carré direct, ça devrait figurer au départ, mais ça apparaît ici :

Citation :
Le plan est muni du repère orthonorme direct (A,\vec{AB},\vec{AD}).

Posté par
lakere : écriture complexe ( isométrie) 01-04-21 à 19:14

Bonsoir Sylvieg

J'avais loupé le coup du repère direct !

Posté par
Hoffnungre : écriture complexe ( isométrie) 04-04-21 à 12:35

bonjour
je suis vraiment  désolé pour le retard voici le reste de l 'énoncé:

b) On pose Z=x+iy ,
montrer que x=\frac{1}{2}(1-f(\alpha )) et y=\frac{1}{2}(1+f(\alpha )) où f() = \frac{cos(\alpha )}{1-sin(\alpha)}
c) Dresser le tableau de variation de f , puis déterminer f(\left]\frac{-\Pi }{4};\frac{\Pi }{2} \right[ )
d) Déterminer l'ensemble des point lorsque varie.
Merci .

Posté par
lakere : écriture complexe ( isométrie) 04-04-21 à 13:02

Bonjour,

Je pense que tu sais maintenant que l'écriture complexe de ton isométrie est :

   z'=i\,e^{i\alpha}z+1+i (et que c'est une rotation).

2)a) Tu résous l'équation z'=z en posant z=x+iy

Posté par
lakere : écriture complexe ( isométrie) 04-04-21 à 13:04

Zut, oubli d'un signe - :

  z'=i\,e^{{\red-}i\alpha}z+1+i

Posté par
Hoffnungre : écriture complexe ( isométrie) 04-04-21 à 13:09

je l'ai résolu comme ça est -ce que c'est correct?
\frac{b}{1-a}=x+iy avec (\frac{b}{1-a} l 'affixe de )

Posté par
lakere : écriture complexe ( isométrie) 04-04-21 à 13:27

Je suppose que  a et b sont définis par z'=az+b

  avec a=i\,e^{-i\alpha} et b=1+i

Si tu es parvenu aux expressions demandées dans l'énoncé pour x et y, pourquoi pas.

Posté par
Hoffnungre : écriture complexe ( isométrie) 04-04-21 à 13:34

oui,
je peine a résoudre la dernière question .

Posté par
lakere : écriture complexe ( isométrie) 04-04-21 à 13:40

As-tu déterminé l'image de l'intervalle \left]-\dfrac{\pi}{4},\dfrac{\pi}{2}\right[ par f ?

Si oui, quel résultat ?

Posté par
lakere : écriture complexe ( isométrie) 04-04-21 à 14:13

J'en rajoute une couche :

- L'image de cet intervalle est primordiale pour répondre à d).

- Pour la déterminer tu n'échapperas pas au calcul de \lim\limits_{\alpha\to\dfrac{\pi}{2}}f(\alpha)

Posté par
Hoffnungre : écriture complexe ( isométrie) 04-04-21 à 22:35

f(\left]\frac{-\Pi }{4},\frac{\Pi}{2}  \right[)=\left]-\infty ,(\sqrt{2}-1) \right[

Posté par
lakere : écriture complexe ( isométrie) 04-04-21 à 22:44

Je pense qu'il y a quelque chose qui ne va pas.
Tu devrais revoir cette partie ( variations de f, limite en \dfrac{\pi}{2}... )

Posté par
Hoffnungre : écriture complexe ( isométrie) 04-04-21 à 23:48

oui,
f est croissante
f(\left]\frac{-\Pi }{4} ;\frac{\Pi }{2}\right[)=(]\sqrt{2}+1);+oo[

Posté par
lakere : écriture complexe ( isométrie) 04-04-21 à 23:59

Toujours pas, mais vois-tu, si tu balances des réponses sans aucune justification, je ne peux que répondre vrai ou faux.

Ici, faux.

Bonne nuit.

Posté par
Hoffnungre : écriture complexe ( isométrie) 05-04-21 à 00:31

f'(x)=\frac{1}{1-sin(x)}
d'ou f est croissante
\lim_{x\rightarrow\frac{-\Pi }{4}}} \frac{cos(x)}{1-sin(x)} = \frac{\sqrt{2}}{2\times (1-\frac{\sqrt{2}}{2})} = \sqrt{2}+1 \\ \lim_{x\rightarrow \frac{\Pi }{2} }\frac{cos(x)}{1-sin(x)}=\lim_{x\rightarrow \frac{\Pi }{2} }\frac{\sqrt{1-sin(x)}}{1-sin(x)} \\                    =\lim_{x\rightarrow \frac{\Pi }{2} }\frac{1}{\sqrt{1-sin(x)}} \\                    =+\infty

Posté par
Sylvieg Moderateurre : écriture complexe ( isométrie) 05-04-21 à 06:53

Bonjour,
Les deux limites sont fausses.
Tu n'as pas le réflexe d'utiliser un grapheur (calculatrice ou autre) pour vérifier tes résultats ?

Posté par
lakere : écriture complexe ( isométrie) 05-04-21 à 11:39

Bonjour,

La première est fausse; c'est un fait.
La seconde  pas vraiment mais la manière d'y parvenir l'est :

   Dans un certain voisinage de \dfrac{\pi}{2}, \cos\,\alpha=\sqrt{1-\sin^{\red 2}\alpha}

   Je préfère écrire : \dfrac{\cos\,\alpha}{1-\sin\,\alpha}=\dfrac{1+\sin\,\alpha}{\cos\,\alpha}

Affaire de goût

Posté par
Hoffnungre : écriture complexe ( isométrie) 05-04-21 à 22:16

oui sin2 !!!j'ai pas fait attention
mais pour la première j'ai vérifié ça me donne le même résultat ,comment la calculer alors?

Posté par
lakere : écriture complexe ( isométrie) 05-04-21 à 22:21

Tu as mal vérifié : \sin\left(-\dfrac{\pi}{4}\right)={\red -}\dfrac{\sqrt{2}}{2}

Posté par
Hoffnungre : écriture complexe ( isométrie) 05-04-21 à 22:30

ouiii, je m'excuse les fautes d'inattention!!
alors c'est f(\left] \frac{-\Pi }{4},\frac{\Pi }{2}\right[)=\left](\sqrt{2}-1),+\infty  \right[

Posté par
lakere : écriture complexe ( isométrie) 05-04-21 à 22:31

Oui

Posté par
lakere : écriture complexe ( isométrie) 06-04-21 à 11:07

Bonjour,

Pour d), tu as le résultat suivant:

    \begin{cases}x=\dfrac{1}{2}[1-f(\alpha)]\\\\y=\dfrac{1}{2}[1+f(\alpha)]\end{cases}

  où x et y représentent les coordonnées de \Omega_{\alpha} en fonction de \alpha

Il n'est pas bien difficile d'éliminer \alpha et même ici f(\alpha) pour obtenir une équation cartésienne de l'ensemble des points \Omega_{\alpha}.
Mais attention, lorsque \alpha décrit \left]-\dfrac{\pi}{4},\dfrac{\pi}{2}\right[, f(\alpha) décrit ]\sqrt{2}-1,+\infty[ en sorte que par exemple l'abscisse x de \Omega_{\alpha} décrit un certain intervalle à déterminer.
Autrement dit, \Omega_{\alpha} ne décrit qu'une partie de l'ensemble dont on a trouvé une équation.

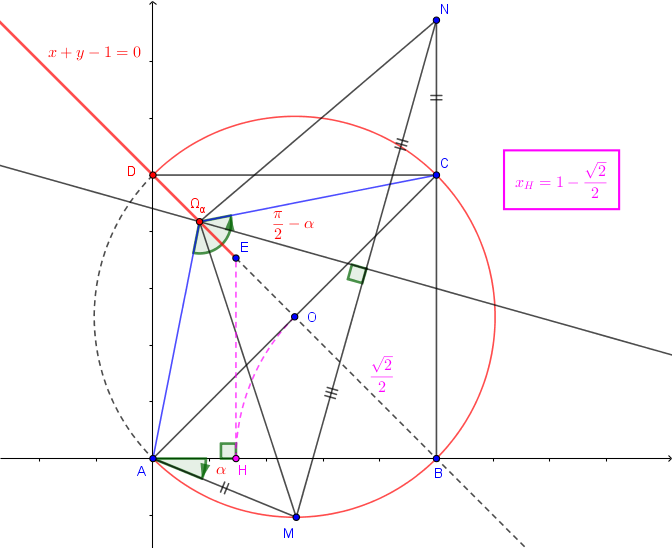
Un dessin :

écriture complexe ( isométrie)


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !