Inscription / Connexion Nouveau Sujet
encadrement solution unique
Bonsoir !
Montrer que l'équation x3 - 3x = 1 admet une solution unique α sur [ - 1 ; 1 ]. Déterminer , un encadrement de α d'amplitude 0,0001
Posons f(x) = x3 - 3x .
f est dérivable, et donc continue, sur IR en tant que fonction polynôme .
∀ x ∈ IR, f '(x) = 3x² - 3 = 3(x² - 1)
f est continue et strictement décroissante sur [ - 1 ; 1 ].
f réalise donc une bijection de [ - 1 ; 1 ] sur l'intervalle image [ - 2 ; 2 ].
or 1 ∈ [ - 2 ; 2 ]
donc l'équation f(x) = 1 admet une solution unique α sur [ - 1 ; 1 ].
Mais, je ne comprends pas comment trouver l'encadrement de la solution unique !
J'ai un exemple sous mes yeux ( sauf qu'il s'agit d'une fonction croissante donc cela doit changer ? ) j'essaye de faire pareil :
f(x)=1 admet une solution unique α sur [-1;1]
1 est compris entre f(1) et f(-1)
donc, c'est la même chose pour α : -1 <α < 1
Déterminons une valeur approchée de α en utilisant la méthode de dichotomie.
on a -1+1 /2 =0 ; f(0)=0 or 0<1 donc f(0)<1 Ainsi, α <0 car f est une fct décroissante et l'ordre est inversé.
Donc, -1 < α < 0
L'utilisation du théorème des valeurs intermédiaires permet alors d'affirmer que l'équation x^3-3x =1 a une solution comprise entre -1 et 0. Cette solution ne peut que être α
On a -1+0 /2 =-0,5 ; f(-0,5) =1,375 donc f(-0,5) > 1 ainsi, -0,5 < α, α > -0,5
Donc -0,5 < α < 0
L'utilisation du théorème des valeurs intermédiaires permet alors d'affirmer que l'équation x^3-3x =1 a une solution comprise entre -0,5 et 0.
On a -0,5/2 = -0,25 ; f(-0,25) =0,734 donc f(-0,25)<1 ainsi, -0,25 > α , α < -0,25
Donc, -0,5< α<-0,25
.... Bon après, je suppose que je suis obligée de faire à la calculatrice, ce serait beaucoup trop long, mais je ne comprends pas comment trouver la solution unique à la calculatrice .. Le tableau de valeur est affichée devant mes yeux mais comment savoir l'encadrement de α ? je suis perdue pour ça ...
je vous remercie
Bonsoir,
il vaut mieux étudier la fct : f(x)=x3-3x-1
et chercher pour quelle valeur unique on a f(x)=0 sur [-1;1].
Tu as le même f '(x) et tu écris :
f est continue et strictement décroissante sur [ - 1 ; 1 ].
f réalise donc une bijection de [ - 1 ; 1 ] sur l'intervalle image [ - 3 ; 1].
or 0 ∈ [ - 3; 1 ]
donc l'équation f(x) = 0 admet une solution unique α sur [ - 1 ; 1 ].
On entre f(x) dans la calculatrice avec :
départ :-1
pas : 0.1
On a : -0.4 <  <-0.3 car f(-0.4)
<-0.3 car f(-0.4)  0.14 et f(-0.3)
0.14 et f(-0.3) -0.13
-0.13
Nouveau départ : -0.14
Pas : 0.01
On trouve : -0.35 <  < -0.34 car ..
< -0.34 car ..
Nouveau départ : -0.35
Pas : 0.001
Tu finis.
Bonsoir Papy Bernie
Merci!
Mais pourquoi prendre la fonction x^3-3x est incorrect ?
J'ai l'impression de tout mélanger, et qu'à chaque fois c'est différent .. :§
Ce n'est pas incorrect, ce n'est pas habituel , c'est tout. Et quand tu vas entrer la fct :
f (x)=x3-3x
dans ta calculatrice avec :
départ : -1
pas : 0.1
ce sera moins facile de voir quand tu passes d'un nb > 1 dans la colonne y à un nb < 1 dans cette même colonne des y.
On repère plus facilement quand on passe d'un nb positif à un nb négatif dans la colonne des y.
Mais fais ta technique , elle est correcte.
Moi, je contunerai à faire la mienne. On trouve le même résultat de toutes façons.
Bonjour, voici un exercice :
Montrer que x^3 - 3x+ 1=0 admet 3 solutions sur R ? Déterminer , un encadrement de chaque solution d'amplitude 5*10^-1 = 1/2 ??
J'ai deja montrer Montrer que x^3 - 3x+ 1=0 admet 3 solutions sur R . il a 3 solutions : le premier dans ]-∞,0] , le deuxieme dans [-1,1] et le troisieme dans [1,+∞[
Bonjour,
tu n'as pas le droit de mettre ton exo sous un autre sauf si le tien a un rapport avec celui qui est au-dessus. Ce qui est le cas ici.
Mais alors , tu écris : "J'ai le même exo mais je ne sais pas trouver les solutions."
OK?
En fait , il faut réduire les intervalles grâce à un graphique fait avec un logiciel par exemple . Voir graph fait avec Sine Qua Non plus bas.
On trouve que les 3 solutions appartiennent à [-2;2].
Avec la touche f(x) , tu rentres dans ta calculatrice :
Y1=x3-3x-1
Tu fais :
Débtable=-2
PasTable=0.5
Puis tu fais :
Table
qui donne :
X.....Y1
-2....-3
-1.5...0.125
Donc : -2 < x1 < -1.5 car f(-2) < 0 et f(-1.5) > 2.
Tu vas trouver x2 et x3 en faisant défiler ton tableau de valeurs.
Graph :
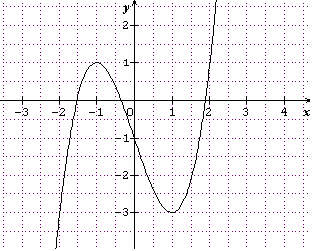
Merci pour votre Aide Monsieur Papy Bernie
c'est ma première fois sur ce site web ... Je suis tellement désolé


