Mon professeur de maths m'a donné un exercice à faire pour jeudi prochain.

On nous donne le programme suivant :

Entrées
Saisir
a,b : bornes de l'intervalle de définition
f : fonction étudiée
N : entier naturel, N 1
Initialisations
pas prend la valeur (b-a)/N
x prend la valeur a
Traitement
Pour k de 0 jusqu'à N
| Marquer le point de coordonnée (x;f(x))
| x prend la valeur x + pas
FinPour

La question de l'exercice est :
Expliquer le rôle et le fonctionnement de cet algorithme.

Or, je comprend le fonctionnement mais je ne sais expliquer le rôle.

Merci d'avance, une élève de seconde.

*** message déplacé ***

Edit Marcel : 1 EXERCICE = 1 TOPIC. Merci de poser les questions d'un même exercice dans son topic.

Tout d'abord, excusez-moi de ne pas avoir respecté les règles du forum.

Ensuite, j'ai demandé à mon professeur de mathématiques quelques explications à propos du rôle d'un programme. Et j'ai donc trouvé le rôle de ce programme !

Mais, à la dernière question de cet exercice on nous demande :
"Traduire le dernier algorithme dans un langage de programmation et tester le programme obtenu."

Le dernier algorithme étant :

Entrées
Saisir
a, b : bornes de l'intervalle de définition
f : fonction étudiée
N : nombre entier naturel, N 1
Initialisations
pas prend la valeur (b-a)/N
x prend la valeur a
Traitement
Pour k de 0 jusqu'à N
| Tracer le segment de (x;f(x))
| à (x+pas; f(x+pas))
|x prend la valeur de x + pas
FinPour

Après quelques recherches sur internet, j'ai trouvé qu'un "langage de programmation est un langage informatique, permettant à un être humain d'écrire un code source qui sera analysé par une machine, généralement un ordinateur."

Donc, si je comprend bien, je dois écrire ce programme sous algobox. Petit problème, c'est seulement la deuxième fois que je me sers d'algobox, et, je n'y arrive pas.
Je ne comprends où sont marqués ;
Entrées
Initialisations
Traitement

En faite, je n'arrive pas tout court à rentrer ce programme dans algobox.

Bonjour,

Je ne sais si c'est un premier exemple d'utilisation d'Algobox mais tu as été gâté(e)

Voici un exemple :

1   VARIABLES
2     a EST_DU_TYPE NOMBRE
3     b EST_DU_TYPE NOMBRE
4     N EST_DU_TYPE NOMBRE
5     pas EST_DU_TYPE NOMBRE
6     k EST_DU_TYPE NOMBRE
7     x EST_DU_TYPE NOMBRE
8   DEBUT_ALGORITHME
9     LIRE a
10    LIRE b
11    LIRE N
12    pas PREND_LA_VALEUR (b-a)/N
13    x PREND_LA_VALEUR a
14    POUR k ALLANT_DE 1 A N
15      DEBUT_POUR
16      TRACER_SEGMENT (x,F1(x))->(x+pas,F1(x+pas))
17      x PREND_LA_VALEUR x+pas
18      FIN_POUR
19  FIN_ALGORITHME

Si la fonction entrée prend les valeurs F1(x)=x*x*x
ce qui s'écrit aussi
F1(x)=pow(x,3)
avec pour
valeur minimale de x : Xmin = a
valeur maximale de x : Xmax = b
valeur minimale de y : Ymin = F1(a)
valeur maximale de y : Ymax = F1(b)

(ce qui suppose que j'aie une bonne idée de la courbe qui représente ici une fonction croissante sur l'intervalle de Xmin à Xmax)

et que je rentre (quand le programme le demande) les valeurs
a = -3
b = 3
N = 24

alors la courbe tracée par Algobox est la suivante :




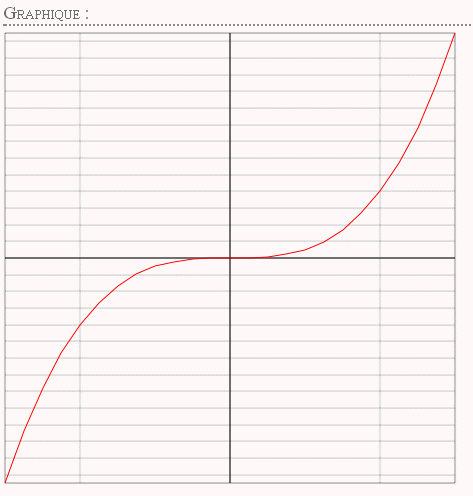
Bon courage !

Bonjour Coll

La manière dont certains profs abordent l'algorithmie me rend perplexe...

A force d'essayer d'aider, j'ai trouvé un tutoriel assez détaillé. Voici le lien

Bonjour borneo !

^{Cela fait sincèrement plaisir de te lire}

Un vif merci. A coup sûr je renverrai parfois à ce texte dont j'ai pris les références.
De ce que je viens de voir rapidement :
. il est très progressif,
. bien illustré,
. raisonnablement expliqué,
. agréablement présenté.

Vraiment de l'excellent travail qui peut être conseillé sans modération.

Merci de me l'avoir fait découvrir !

Merci à Coll pour t'es explications détaillées. Elles m'ont été très utile.
Merci aussi à Borneo pour ce site vraiment super.